搜索
【题目】如图,△ABC中,AB=AC,∠BAC=90°,D是BC边上任意一点,求证：BD
+CD=2AD.
参考答案：
【答案】见解析
【解析】
作AE⊥BC于E，由于∠BAC=90°，AB=AC，所以BE=CE，要证明BD
+CD=2AD，只需找出BD、CD、AD三者之间的关系即可，由勾股定理可得出AD=AE+ED，AE=AB-BE=AC-CE，ED=BD-BE=CE-CD，代入求出三者之间的关系即可得证．
证明：作AE⊥BC于E，如图所示：
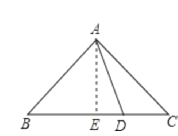
由题意得：ED=BDBE=CECD，
∵在△ABC中,∠BAC=90°，AB=AC，
∴BE=CE=
BC，
由勾股定理可得：
AB+AC=BC，
AE=ABBE=ACCE，，
AD=AE+ED，
2ADimg src="http://thumb.zyjl.cn/questionBank/Upload/2020/11/22/06/793bb150/SYS202011220603314423751839_DA/SYS202011220603314423751839_DA.001.png" width="11" height="20" style="-aw-left-pos:0pt; -aw-rel-hpos:column; -aw-rel-vpos:paragraph; -aw-top-pos:0pt; -aw-wrap-type:inline" />=2AE+2ED=ABBE+(BDBE) +ACCE+(CECD)
=AB+AC+BD+CD2BD×BE2CD×CE=AB+AC+BD+CD2×BC×BC
=BD+CD,
即,BD+CD=2AD
-
科目： 来源： 题型：
查看答案和解析>>【题目】（1）图（1）是一个长为2m，宽为2n的矩形，把此矩形沿图中虚线用剪刀均分为四个小长方形，然后按图（2）的形状拼成一个大正方形．请问：这两个图形的什么量不变？
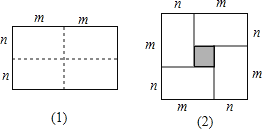
（2）把所得的大正方形面积比原矩形的面积多出的阴影部分的面积用含m，n的代数式表示为（m-n）2或m2-2mn+n2 ．
（3）由前面的探索可得出的结论是：在周长一定的矩形中，当 时，面积最大．
（4）若矩形的周长为24cm，则当边长为多少时，该图形的面积最大？最大面积是多少？ -
科目： 来源： 题型：
查看答案和解析>>【题目】一个不透明的袋子中装有三个完全相同的小球，分别标有数字3、4、5．从袋子中随机取出一个小球，用小球上的数字作为十位的数字，然后放回；再取出一个小球，用小球上的数字作为个位上的数字，这样组成一个两位数，试问：按这种方法能组成哪些位数？十位上的数字与个位上的数字之和为9的两位数的概率是多少？用列表法或画树状图法加以说明．
-
科目： 来源： 题型：
查看答案和解析>>【题目】计算：
（1）23－17－（－7）＋（－16）；
（2）
（3）
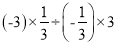
（4）
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知，如图，在Rt△ABC中，∠ACB=90°，AE平分∠BAC交BC于点E，D为AC上的点，BE=DE．
（1）求证：∠B+∠EDA=180°；
（2）求
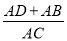的值。．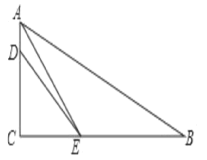
-
科目： 来源： 题型：
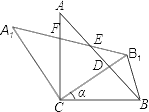
查看答案和解析>>【题目】如图，△ABC中，∠ACB＝90，AC＝BC，将△ABC绕点C逆时针旋转α角（0＜α＜90）得到△A1B1C，连结BB1.设CB1交AB于D，A1B1分别交AB、AC于E、F，
（1）在图中不再添加其它任何线段的情况下，请你找出一对全等的三角形，并加以证明（△ABC与△A1B1C全等除外）；
（2）当△BB1D是等腰三角形时，求α.
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，正方形ABCD中，AB=3，点E在边CD上，且CD=3DE，将△ADE沿AE对折至△AFE，延长EF交边BC于点G，连接AG、CF．下列结论：①点G是BC中点；②FG=FC；③与∠AGB相等的角有5个；④S△FGC=
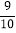．其中正确的是（ ）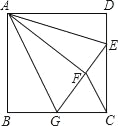
A. ①③ B. ②③ C. ①④ D. ②④
相关试题
