【题目】荣庆公司计划从商店购买同一品牌的台灯和手电筒,已知购买一个台灯比购买一个手电筒多用20元,若用400元购买台灯和用160元购买手电筒,则购买台灯的个数是购买手电筒个数的一半.
(1)求购买该品牌一个台灯、一个手电筒各需要多少元?
(2)经商谈,商店给予荣庆公司购买一个该品牌台灯赠送一个该品牌手电筒的优惠,如果荣庆公司需要手电筒的个数是台灯个数的2倍还多8个,且该公司购买台灯和手电筒的总费用不超过670元,那么荣庆公司最多可购买多少个该品牌台灯?
参考答案:
【答案】(1)购买一个台灯需要25元,购买一个手电筒需要5元;
(2)荣庆公司最多可购买21个该品牌的台灯.
【解析】
试题(1)设购买该品牌一个手电筒需要x元,则购买一个台灯需要(x+20)元.则根据等量关系:购买台灯的个数是购买手电筒个数的一半,列出方程;
(2)设公司购买台灯的个数为a各,则还需要购买手电筒的个数是(2a+8)个,则根据“该公司购买台灯和手电筒的总费用不超过670元”列出不等式.
试题解析:(1)设购买该品牌一个手电筒需要x元,则购买一个台灯需要(x+20)元.
根据题意 得![]()
解得 x=5
经检验,x=5是原方程的解.
所以 x+20=25.
答:购买一个台灯需要25元,购买一个手电筒需要5元;
(2)设公司购买台灯的个数为a,则还需要购买手电筒的个数是(2a+8)
由题意得 25a+5(2a+8)≤670
解得 a≤21
所以 荣庆公司最多可购买21个该品牌的台灯.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:
(1)|-2|÷(-
 )+(-5)×(-2); (2)(
)+(-5)×(-2); (2)( -
- +
+ )×(-24);
)×(-24);(3)15÷(-
 +
+ ); (4)(-2)2-|-7|-3÷(-
); (4)(-2)2-|-7|-3÷(-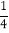 )+(-3)3×(-
)+(-3)3×(- )2.
)2. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知抛物线y=﹣x2+2x+3与坐标轴交于A,B,C三点,抛物线上的点D与点C关于它的对称轴对称.
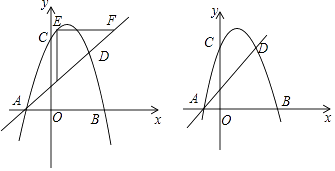
(1)直接写出点D的坐标和直线AD的解析式;
(2)点E是抛物线上位于直线AD上方的动点,过点E分别作EF∥x轴,EG∥y轴并交直线AD于点F、G,求△EFG周长的最大值;
(3)若点P为y轴上的动点,则在抛物线上是否存在点Q,使得以A,D,P,Q为顶点的四边形是平行四边形?若存在,请求出点Q的坐标,若不存在,请说明理由. -
科目: 来源: 题型:
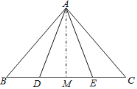
查看答案和解析>>【题目】如图,△ABC中,∠C=90°,∠A=30°.

(1)用尺规作图作AB边上的中垂线DE,交AC于点D,交AB于点E.(保留作图痕迹,不要求写作法和证明);
(2)连接BD,求证:BD平分∠CBA.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知点
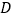 、
、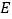 在
在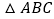 的
的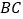 边上,
边上,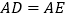 ,
,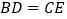 ,为了判断
,为了判断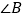 与
与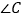 的大小关系,请你填空完成下面的推理过程,并在空白括号内,注明推理的根据.
的大小关系,请你填空完成下面的推理过程,并在空白括号内,注明推理的根据.解:作
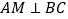 ,垂足为
,垂足为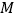
∵
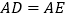 ,
,∴
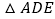 是________三角形,
是________三角形,∴
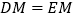 ________
________又∵
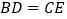 ,
,∴
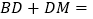 ________,即
________,即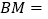 ________;
________;又∵________(自己所作),
∴
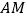 是线段________的垂直平分线;
是线段________的垂直平分线;∴
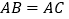 ________
________∴________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】函数y=x2+bx+c与y=x的图象如图所示,有以下结论: ①b2﹣4c>0;
②b+c+1=0;
③3b+c+6=0;
④当1<x<3时,x2+(b﹣1)x+c<0.
其中正确的个数为( )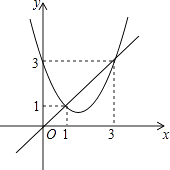
A.1个
B.2个
C.3个
D.4个 -
科目: 来源: 题型:
查看答案和解析>>【题目】观察下列等式 12=1=
 ×1×2×(2+1)
×1×2×(2+1)
12+22= ×2×3×(4+1)
×2×3×(4+1)
12+22+32= ×3×4×(6+1)
×3×4×(6+1)
12+22+32+42= ×4×5×(8+1)…
×4×5×(8+1)…
可以推测12+22+32+…+n2= .
相关试题

