Question

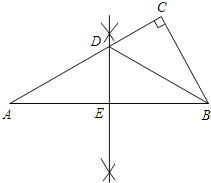
【题目】如图，△ABC中，∠C=90°，∠A=30°．

（1）用尺规作图作AB边上的中垂线DE，交AC于点D，交AB于点E．（保留作图痕迹，不要求写作法和证明）；

（2）连接BD，求证：BD平分∠CBA．

Answer 1

【答案】（1）作图见解析；（2）证明见解析．

【解析】试题分析：（1）分别以A、B为圆心，以大于AB的长度为半径画弧，过两弧的交点作直线，交AC于点D，AB于点E，直线DE就是所要作的AB边上的中垂线；

（2）根据线段垂直平分线上的点到线段两端点的距离相等可得AD=BD，再根据等边对等角的性质求出∠ABD=∠A=30°，然后求出∠CBD=30°，从而得到BD平分∠CBA．

试题解析：（1）解：如图所示，DE就是要求作的AB边上的中垂线；

（2）证明：∵DE是AB边上的中垂线，∠A=30°，

∴AD=BD，

∴∠ABD=∠A=30°，

∵∠C=90°，

∴∠ABC=90°-∠A=90°-30°=60°，

∴∠CBD=∠ABC-∠ABD=60°-30°=30°，

∴∠ABD=∠CBD，

∴BD平分∠CBA．