【题目】如图,在平面直角坐标系中,O为坐标原点,已知点F(2 ![]() ,0),直角GF交y轴正半轴于点G,且∠GFO=30°.
,0),直角GF交y轴正半轴于点G,且∠GFO=30°. 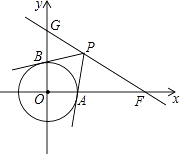
(1)请直接写出点G的坐标;
(2)若⊙O的半径为1,点P是直线GF上的动点,直线PA、PB分别与⊙O相切于点A、B.
①求切线长PB的最小值;
②在直线GF上是否存在点P,使得∠APB=60°?若存在,请求出点P的坐标;若不存在,请说明理由.
参考答案:
【答案】
(1)解:∵F(2 ![]() ,0),
,0),
∴OF=2 ![]() ,
,
∵∠GFO=30°,
∴OG=2,
∴点G的坐标是(0,2)
(2)解:①连接OPOP,如图,
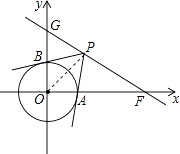
∵PB切⊙OO于点BB,
∴OB⊥PB,
根据勾股定理得PB2=OP2﹣OB2,
∵OB=1,
∴要使BP的值最小,则需OP的值最小,当OP⊥GF时,线段PO最短,
在Rt△PFO,OF=2 ![]() ,∠GFO=30°,
,∠GFO=30°,
∴OP= ![]() ,
,
∴PB= ![]() =
= ![]() =
= ![]() ;
;
②存在,
∵PA、PB均与⊙O相切,
∴OP平分∠APB,
∵∠APB=60°,
∴∠OPB=30°,
∵OB=1,∴OP=2,
∴点P是以点O为圆心,2为半径的圆与直线GF的交点,
即图中的P1、P2两点,连接OP2,
∵OG=2,
∴点P1与点G(0,2)重合,即P1(0,2),
在Rt△GOF中,∠GFO=30°,
∴∠OGF=60°,
∵OG=OP2,
∴△GOP2是等边三角形,
∴GP2=OG=2,已知GF=4,
∴FP2=2,
∴P2为GF的中点,
∴P2( ![]() ,1),
,1),
综上所述,满足条件的点P的坐标为(0,2)或( ![]() ,1).
,1).
【解析】(1)由已知条件得到OF=2 ![]() ,解直角三角形即可得到结论;(2)①连接OPOP,根据切线的性质得到OB⊥PB,当OP⊥GF时,线段PO最短,解直角三角形得到OP=
,解直角三角形即可得到结论;(2)①连接OPOP,根据切线的性质得到OB⊥PB,当OP⊥GF时,线段PO最短,解直角三角形得到OP= ![]() ,PB=
,PB= ![]() =
= ![]() =2;
=2;
②根据切线的性质和角平分线的定义得到∠OPB=30°,求得OP=2,点P是以点O为圆心,2为半径的圆与直线GF的交点,由于点P1与点G(0,2)重合,即P1(0,2),推出△GOP2是等边三角形求得FP2=2,即可得到结论.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=﹣x2+bx+c的顶点为Q,抛物线与x轴交于A(﹣1,0),B(5,0)两点,与y轴交于点C.
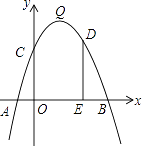
(1)求抛物线的解析式及其顶点Q的坐标;
(2)在该抛物线上求一点P,使得S△PAB=S△ABC , 求出点P的坐标:
(3)若点D是第一象限抛物线上的一个动点,过点D作DE⊥x轴,垂足为E.有一个同学说:“在第一象限抛物线上的所有点中,抛物线的顶点Q与x轴相距最远,所以当点D运动至点Q时,折线D﹣E﹣O的长度最长.”这个同学的说法正确吗?请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知一次函数 y =ax+b的图象经过点 A (1,3)且与 y =2x-3 平行.
(1)求出 a ,b .写出 y与 x的函数关系;
(2)求当 x =-2 时,y的值;当 y =9时,x的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】方程6x2﹣5=0的一次项系数是( )
A.6B.5C.﹣5D.0
-
科目: 来源: 题型:
查看答案和解析>>【题目】抛物线y=﹣x2向右平移1个单位,再向上平移2个单位得到( )
A.y=﹣(x﹣1)2+2B.y=﹣(x+1)2+2
C.y=﹣(x﹣1)2﹣2D.y=﹣(x+1)2﹣2
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知在
 中,
中, 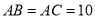 ,
, 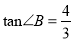 .
.(1)求
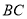 的长;
的长;(2)点D在边AB上,且AD=1,
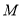 为边
为边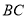 上一动点,连接DM.当
上一动点,连接DM.当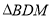 是直角三角形时,求BM的长.
是直角三角形时,求BM的长.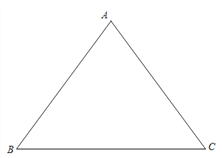
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数
 与一次函数
与一次函数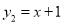 ,令W=
,令W=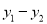 .
.(1)若
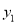 、
、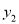 的函数图像交于x轴上的同一点.
的函数图像交于x轴上的同一点.①求
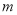 的值;
的值;②当
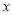 为何值时,W的值最小,试求出该最小值;
为何值时,W的值最小,试求出该最小值;(2)当
 时,W随x的增大而减小.
时,W随x的增大而减小.①求
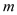 的取值范围;
的取值范围;②求证:
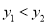 .
.
相关试题

