【题目】已知二次函数![]() 与一次函数
与一次函数![]() ,令W=
,令W=![]() .
.
(1)若![]() 、
、![]() 的函数图像交于x轴上的同一点.
的函数图像交于x轴上的同一点.
①求![]() 的值;
的值;
②当![]() 为何值时,W的值最小,试求出该最小值;
为何值时,W的值最小,试求出该最小值;
(2)当![]() 时,W随x的增大而减小.
时,W随x的增大而减小.
①求![]() 的取值范围;
的取值范围;
②求证: ![]() .
.
参考答案:
【答案】(1)①![]() 的值为1;②W的最小值是
的值为1;②W的最小值是![]() ;
;
(2)①![]() 的取值范围是
的取值范围是![]() ;②证明见解析.
;②证明见解析.
【解析】试题分析:(1)①y2=x+1与x轴的交点为(-1,0),再把(-1,0)代入二次函数y1=mx2-2mx-3(m>0)中得,m=1;②把函数解析式代入w=y1-y2中得w=x2-2x-3-x-1=x2-3x-4=(x-![]() ,则当x=
,则当x=![]() 时,W有最小值为
时,W有最小值为![]() ;(2)由W=y1-y2得:
;(2)由W=y1-y2得:![]() ,所以对称轴为
,所以对称轴为![]() ,又由m>0,
,又由m>0, ![]() 时,且W随x的增大而减小得:
时,且W随x的增大而减小得:![]() ,所以
,所以![]() ;②当x=-2时,
;②当x=-2时,![]() ,当
,当![]() 时,W随x的增大而减小. 所以,
时,W随x的增大而减小. 所以, ![]() ;由
;由![]() ,所以
,所以![]() ,即
,即![]() ;
;
所以![]() ,即
,即![]() <0,所以
<0,所以![]() ;
;
试题解析:
(1)①∵y2=x+1与x轴的交点为(-1,0)
∴把(-1,0)代入二次函数y1=mx2-2mx-3(m>0)中得,m=1
②w=y1-y2中得w=x2-2x-3-x-1=x2-3x-4=(x-![]() ,则当x=
,则当x=![]() 时,W有最小值为
时,W有最小值为![]() ;
;
(2)①![]()
对称轴为![]()
因为![]() ,
, ![]() 时,且W随x的增大而减小.
时,且W随x的增大而减小.
所以,![]() ,
,
所以![]()
所以![]()
②当x=-2时,![]()
因为![]() 时,W随x的增大而减小.
时,W随x的增大而减小.
所以, ![]()
因为![]() ,所以
,所以![]() ,即
,即![]()
所以![]() ,即
,即![]() <0,所以
<0,所以![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,O为坐标原点,已知点F(2
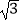 ,0),直角GF交y轴正半轴于点G,且∠GFO=30°.
,0),直角GF交y轴正半轴于点G,且∠GFO=30°. 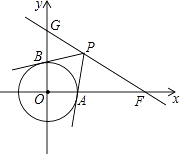
(1)请直接写出点G的坐标;
(2)若⊙O的半径为1,点P是直线GF上的动点,直线PA、PB分别与⊙O相切于点A、B.
①求切线长PB的最小值;
②在直线GF上是否存在点P,使得∠APB=60°?若存在,请求出点P的坐标;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】抛物线y=﹣x2向右平移1个单位,再向上平移2个单位得到( )
A.y=﹣(x﹣1)2+2B.y=﹣(x+1)2+2
C.y=﹣(x﹣1)2﹣2D.y=﹣(x+1)2﹣2
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知在
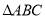 中,
中, 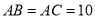 ,
, 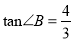 .
.(1)求
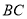 的长;
的长;(2)点D在边AB上,且AD=1,
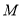 为边
为边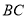 上一动点,连接DM.当
上一动点,连接DM.当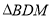 是直角三角形时,求BM的长.
是直角三角形时,求BM的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】分解因式:x3﹣x2﹣20x= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】抛物线y=2(x﹣2)2+4的顶点坐标为_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】声速y(米/秒)与气温x(℃)之间的关系如下表所示:
气温x(℃)
0
5
10
15
20
音速y(米/秒)
331
334
337
340
343
从表中可知音速y随温度x的升高而升高,在气温为20℃的一天召开运动会,某人看到发令枪的烟0.2秒后,听到了枪声,请问此人距发令地点约有多少米?
相关试题

