【题目】如图,抛物线y=﹣x2+bx+c的顶点为Q,抛物线与x轴交于A(﹣1,0),B(5,0)两点,与y轴交于点C.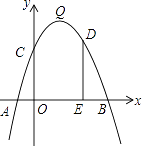
(1)求抛物线的解析式及其顶点Q的坐标;
(2)在该抛物线上求一点P,使得S△PAB=S△ABC , 求出点P的坐标:
(3)若点D是第一象限抛物线上的一个动点,过点D作DE⊥x轴,垂足为E.有一个同学说:“在第一象限抛物线上的所有点中,抛物线的顶点Q与x轴相距最远,所以当点D运动至点Q时,折线D﹣E﹣O的长度最长.”这个同学的说法正确吗?请说明理由.
参考答案:
【答案】
(1)
解:∵抛物线y=﹣x2+bx+c与x轴交于A(﹣1,0),B(5,0)两点,
∴y=﹣(x+1)(x﹣5)=﹣x2+4x+5,
∴抛物线的解析为y=﹣x2+4x+5;
∵y=﹣x2+4x+5=﹣(x﹣2)2+9,
∴顶点Q的坐标为(2,9)
(2)
解:在y=﹣x2+4x+5中,当x=0时,y=5,
∴点C的坐标为:(0,5),
设点P的纵坐标为a,
若S△PAB=S△ABC,则|a|=5,
解得a=±5.
当a=5时,﹣x2+4x+5=5,解得x=0(舍去)或x=4,此时点p的坐标为(4,5);
当a=﹣5时,﹣x2+4x+5=﹣5,解得x=2± ![]() ,此时点p的坐标为(2+
,此时点p的坐标为(2+ ![]() ,﹣5)或(2﹣
,﹣5)或(2﹣ ![]() ,﹣5);
,﹣5);
综上,点p的坐标为(4,5)或(2+ ![]() ,﹣5)或(2﹣
,﹣5)或(2﹣ ![]() ,﹣5)
,﹣5)
(3)
解:这个同学的说法不正确
理由:设D(t,﹣t2+4t+5),折线D﹣E﹣O的长度为L,
则L=﹣t2+4t+5+t=﹣(t﹣ ![]() )2+
)2+ ![]() .
.
∵a<0,
∴当t= ![]() 时,L最大值=
时,L最大值= ![]() .
.
而当点D与点Q重合时,L=9+2=11< ![]() ,
,
∴该同学的说法不正确
【解析】(1)由抛物线y=﹣x2+bx+c与x轴交于A(﹣1,0),B(5,0)两点,可直接利用交点式求得y=﹣(x+1)(x﹣5)=﹣x2+4x+5,继而求得顶点Q的坐标;(2)首先设点P的纵坐标为a,由S△PAB=S△ABC , 可得a=±5,然后可得﹣x2+4x+5=±5,继而求得点P的坐标;(3)首先设D(t,﹣t2+4t+5),折线D﹣E﹣O的长度为L,则可得L=﹣t2+4t+5+t,然后求得最大值,即可知这个同学的是否说法正确.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在一个不透明袋子中有1个红球、1 个绿球和n个白球,这些球除颜色外都相同.
(1)从袋中随机摸出1个球,记录下颜色后放回袋子中并搅匀.经大量试验,发现摸到白球的频率稳定在0.75左右,求n的值;
(2)当n=2时,把袋中的球搅匀后任意摸出2个球,用树状图或列表求摸出的2个球颜色不同的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算5x﹣3y﹣(2x﹣9y)结果正确的是( )
A.7x﹣6y
B.3x﹣12y
C.3x+6y
D.9xy -
科目: 来源: 题型:
查看答案和解析>>【题目】将抛物线y=x2﹣2x+3向左平移2个单位长度后,得到的抛物线的解析式为( )
A.y=(x﹣1)2+2B.y=(x+1)2+2C.y=(x+3)2+2D.y=(x﹣3)2+2
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知一次函数 y =ax+b的图象经过点 A (1,3)且与 y =2x-3 平行.
(1)求出 a ,b .写出 y与 x的函数关系;
(2)求当 x =-2 时,y的值;当 y =9时,x的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】方程6x2﹣5=0的一次项系数是( )
A.6B.5C.﹣5D.0
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,O为坐标原点,已知点F(2
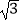 ,0),直角GF交y轴正半轴于点G,且∠GFO=30°.
,0),直角GF交y轴正半轴于点G,且∠GFO=30°. 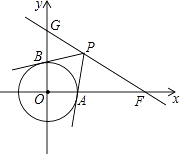
(1)请直接写出点G的坐标;
(2)若⊙O的半径为1,点P是直线GF上的动点,直线PA、PB分别与⊙O相切于点A、B.
①求切线长PB的最小值;
②在直线GF上是否存在点P,使得∠APB=60°?若存在,请求出点P的坐标;若不存在,请说明理由.
相关试题

