【题目】如图,在△ABC中,AB=AC,∠A=36°,BD平分∠ABC交AC于点D.求证:AD=BC
证明:∵AB=AC
∴∠ABC=∠C ( )
∵∠A=36°
又∵∠A+∠ABC+∠C=180° ( )
∴∠ABC= °
∵BD平分∠ABC
∴∠1=∠2= °
∴∠C=∠ =72°
∴AD= ,BC= ( )
∴AD=BC

参考答案:
【答案】等边对等角,三角形内角和定理,72,36,BDC,BD,BD,等角对等边
【解析】
根据等腰三角形的性质得到∠ABC=C=72°,根据角平分线的定义得到∠ABD=∠DBC=36°,∠BDC=72°,根据等腰三角形的判定即可得到结论.
证明:∵AB=AC
∴∠ABC=∠C ( 等边对等角)
∵∠A=36°
又∵∠A+∠ABC+∠C=180° ( 三角形内角和定理)
∴∠ABC=72°
∵BD平分∠ABC
∴∠1=∠2=36°
∴∠C=∠BDC=72°
∴AD=BD,BC=BD( 等角对等边)
∴AD=BC.
故答案为:等边对等角,三角形内角和定理,72,36,BDC,BD,BD,等角对等边.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,已知四边形ABCD、ADEF都是菱形,∠BAD=∠FAD, ∠BAD为锐角.
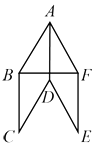
(1)求证:AD⊥BF;
(2)若BF=BC,求∠ADC的度数。 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,O是直线AB上一点,OC为任意一条射线,OD平分∠BOC,OE平分∠AOC.

(1)指出图中∠AOD与∠BOE的补角;
(2)试判断∠COD与∠COE具有怎样的数量关系.并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,在△ABC中,D是AC上一点,E是AB上一点,且∠AED=∠C.
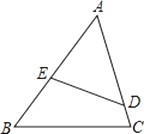
(1)求证:△AED∽△ACB;
(2)若AB=6,AD=4,AC=5,求AE的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】我们知道,对于一个图形,通过两种不同的方法计算它的面积,可以得到一个数学等式.例如构造图1可以得到
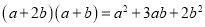 .请解答下列问题:
.请解答下列问题: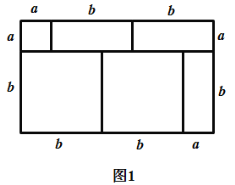
(1)仿照图1,构造适当的图形得到
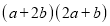 的值;
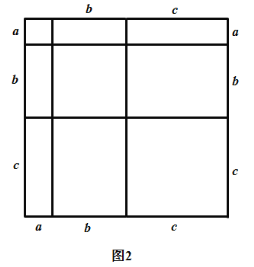
的值;(2)写出图2中所表示的数学等式;
(3)利用(2)中所得到的结论,解决下面的问题:己知
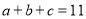 ,
, ,求
,求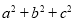 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知,直线
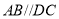 ,点
,点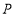 为平面上一点,连接
为平面上一点,连接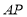 与
与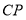 .
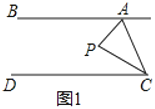
.(1)如图1,点
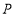 在直线
在直线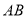 、
、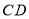 之间,当
之间,当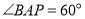 ,
,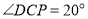 时,求
时,求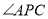 .
.
(2)如图2,点
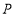 在直线
在直线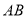 、
、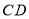 之间
之间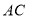 左侧,
左侧,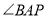 与
与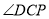 的角平分线相交于点
的角平分线相交于点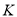 ,写出
,写出 与
与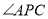 之间的数量关系,并说明理由.
之间的数量关系,并说明理由.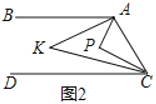
(3)如图3,点
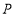 落在
落在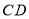 下方,
下方,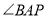 与
与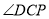 的角平分线相交于点
的角平分线相交于点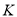 ,
, 与
与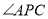 有何数量关系?并说明理由.
有何数量关系?并说明理由.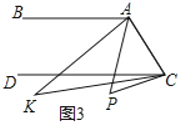
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD是平行四边形,点A(1,0)、B(3,1)、C(3,3);反比例函数
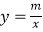 (x>0)的图象经过点D,点P是一次函数 y=kx+33k (k≠0)的图象与该反比例函数图象的一个公共点.
(x>0)的图象经过点D,点P是一次函数 y=kx+33k (k≠0)的图象与该反比例函数图象的一个公共点.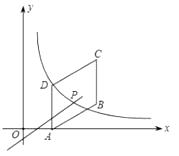
(1)求反比例函数的关系式;
(2)通过计算:说明一次函数 y=kx+33k 的图象一定经过点C;
(3)当一次函数 y=kx+33k 的图象平分平行四边形ABCD的面积时,求此一次函数的关系式。
相关试题

