【题目】已知:如图,在△ABC中,D是AC上一点,E是AB上一点,且∠AED=∠C.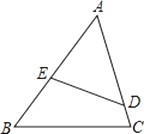
(1)求证:△AED∽△ACB;
(2)若AB=6,AD=4,AC=5,求AE的长.
参考答案:
【答案】
(1)证明:∵∠AED=∠C,∠A=∠A,
∴△AED∽△ACB.
(2)解:∵△AED∽△ACB,
∴AE:AC=AD:AB,
∵AB=6,AD=4,AC=5,
∴AE= ![]() ,
,
∴BE=AB-AE= ![]() .
.
【解析】(1)根据相似三角形的判定:两个角对应相等的两个三角形相似.
(2)由相似三角形的性质得对应边的比相等,即可求出AE的长,再由BE=AB-AE即可求出答案.
【考点精析】通过灵活运用相似三角形的判定与性质,掌握相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比等于相似比;相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方即可以解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(3分)如图,AD是△ABC的角平分线,DE⊥AC,垂足为E,BF∥AC交ED的延长线于点F,若BC恰好平分∠ABF,AE=2BF.给出下列四个结论:①DE=DF;②DB=DC;③AD⊥BC;④AC=3BF,其中正确的结论共有( )

A. 4个 B. 3个 C. 2个 D. 1个
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,已知四边形ABCD、ADEF都是菱形,∠BAD=∠FAD, ∠BAD为锐角.
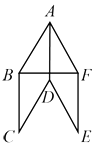
(1)求证:AD⊥BF;
(2)若BF=BC,求∠ADC的度数。 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,O是直线AB上一点,OC为任意一条射线,OD平分∠BOC,OE平分∠AOC.

(1)指出图中∠AOD与∠BOE的补角;
(2)试判断∠COD与∠COE具有怎样的数量关系.并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,∠A=36°,BD平分∠ABC交AC于点D.求证:AD=BC
证明:∵AB=AC
∴∠ABC=∠C ( )
∵∠A=36°
又∵∠A+∠ABC+∠C=180° ( )
∴∠ABC= °
∵BD平分∠ABC
∴∠1=∠2= °
∴∠C=∠ =72°
∴AD= ,BC= ( )
∴AD=BC

-
科目: 来源: 题型:
查看答案和解析>>【题目】我们知道,对于一个图形,通过两种不同的方法计算它的面积,可以得到一个数学等式.例如构造图1可以得到
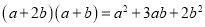 .请解答下列问题:
.请解答下列问题: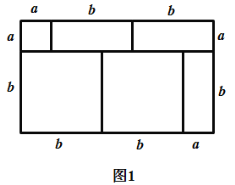
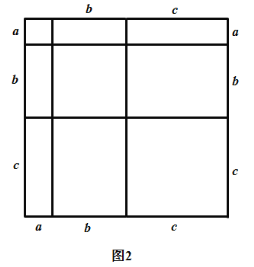
(1)仿照图1,构造适当的图形得到
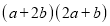 的值;
的值;(2)写出图2中所表示的数学等式;
(3)利用(2)中所得到的结论,解决下面的问题:己知
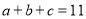 ,
, ,求
,求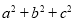 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知,直线
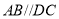 ,点
,点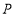 为平面上一点,连接
为平面上一点,连接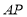 与
与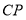 .
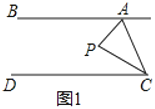
.(1)如图1,点
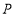 在直线
在直线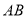 、
、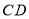 之间,当
之间,当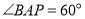 ,
,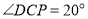 时,求
时,求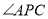 .
.
(2)如图2,点
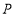 在直线
在直线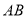 、
、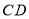 之间
之间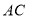 左侧,
左侧,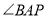 与
与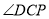 的角平分线相交于点
的角平分线相交于点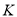 ,写出
,写出 与
与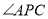 之间的数量关系,并说明理由.
之间的数量关系,并说明理由.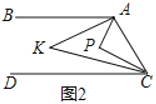
(3)如图3,点
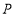 落在
落在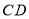 下方,
下方,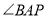 与
与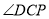 的角平分线相交于点
的角平分线相交于点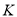 ,
, 与
与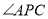 有何数量关系?并说明理由.
有何数量关系?并说明理由.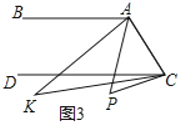
相关试题

