搜索
【题目】已知，直线
，点
为平面上一点，连接
与
．
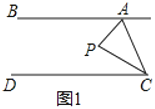
（1）如图1，点在直线
、
之间，当
，
时，求
．
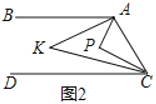
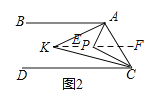
（2）如图2，点在直线、之间
左侧，
与
的角平分线相交于点
，写出
与之间的数量关系，并说明理由．
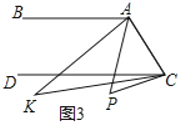
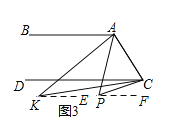
（3）如图3，点落在下方，与的角平分线相交于点，与有何数量关系？并说明理由．
参考答案：
【答案】（1）
；（2）
，见详解；（3），见详解
【解析】
（1）过点P作
，根据平行线的性质得到
，再根据
计算即可；
（2）过K作
，根据平行线的性质和角平分线的定义可得出
与
的数量关系；
（3）过K作，根据平行线的性质和角平分线的定义可得出与的数量关系.
（1）(如图1，过点P作
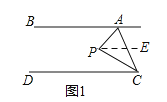
（2）
如图2，过K作
过点P作
同理可得
与
的角平分线相交于点K
（3）
如图3，过K作
过点P作
同理可得
与的角平分线相交于点K
-
科目： 来源： 题型：
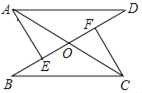
查看答案和解析>>【题目】如图，已知AC、BD相交于点O，AD＝BC，AE⊥BD于点E，CF⊥BD于点F，BE＝DF．求证：
（1）△ADE≌△CBF；
（2）OA＝OC．
-
科目： 来源： 题型：
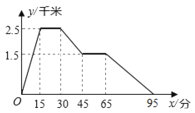
查看答案和解析>>【题目】如图所示：图象中所反映的过程是：小冬从家跑步去体育场，在那里锻炼了一阵后，又去早餐店吃早餐，然后散步走回家．其中x轴表示时间，y轴表示小冬离家的距离．根据图象提供的信息，下列说法正确的有________.
①．体育场离小冬家2.5千米 ②．小冬在体育场锻炼了15分钟
③．体育场离早餐店4千米 ④．小冬从早餐店回家的平均速度是3千米/小时
-
科目： 来源： 题型：
查看答案和解析>>【题目】给出下面两个定理:
①线段垂直平分线上的点到这条线段两个端点的距离相等;
②到一条线段两个端点距离相等的点在这条线段的垂直平分线上.
应用上述定理进行如下推理:
如图,直线l是线段MN的垂直平分线.
∵点A在直线l上,∴AM=AN.( )
∵BM=BN,∴点B在直线l上.( )
∵CM≠CN,∴点C不在直线l上.
这是∵如果点C在直线l上,那么CM=CN, ( )
这与条件CM≠CN矛盾.
以上推理中各括号内应注明的理由依次是 ( )
A. ②①① B. ②①②
C. ①②② D. ①②①
-
科目： 来源： 题型：
查看答案和解析>>【题目】近年来，我国煤矿安全事故频频发生，其中危害最大的是瓦斯，其主要成分是CO．在一次矿难事件的调查中发现：从零时起，井内空气中CO的浓度达到4mg/L，此后浓度呈直线型增加，在第7小时达到最高值46mg/L，发生爆炸；爆炸后，空气中的CO浓度成反比例下降．如图所示，根据题中相关信息回答下列问题：
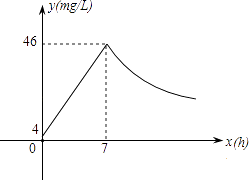
（1）求爆炸前后空气中CO浓度y与时间x的函数关系式，并写出相应的自变量取值范围；
（2）当空气中的CO浓度达到34mg/L时，井下3km的矿工接到自动报警信号，这时他们至少要以多少km/h的速度撤离才能在爆炸前逃生？
（3）矿工只有在空气中的CO浓度降到4mg/L及以下时，才能回到矿井开展生产自救，求矿工至少在爆炸后多少小时才能下井？ -
科目： 来源： 题型：
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,AD是△ABC的角平分线,DE⊥AB,DF⊥AC,垂足分别为E,F.则下列结论:①AD上任意一点到点C,B的距离相等;②AD上任意一点到边AB,AC的距离相等;③BD=CD,AD⊥BC;④∠BDE=∠CDF.其中正确的个数为（ ）
A. 4 B. 3 C. 2 D. 1
-
科目： 来源： 题型：
查看答案和解析>>【题目】某商场销售每个进价为150元和120元的A、B两种型号的足球，如表是近两周的销售情况：
销售时段
销售数量
销售收入
A种型号
B种型号
第一周
3个
4个
1200元
第二周
5个
3个
1450元
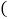进价、售价均保持不变，利润
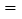销售收入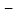
进货成本
(1)求A、B两种型号的足球的销售单价；
(2)若商场准备用不多于8400元的金额再购进这两种型号的足球共60个，求A种型号的足球最多能采购多少个？
(3)在
的条件下，商场销售完这60个足球能否实现利润超过2550元，若能，请给出相应的采购方案；若不能请说明理由．
相关试题
