【题目】如图所示,已知四边形ABCD、ADEF都是菱形,∠BAD=∠FAD, ∠BAD为锐角.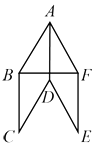
(1)求证:AD⊥BF;
(2)若BF=BC,求∠ADC的度数。
参考答案:
【答案】
(1)证明:∵四边形ABCD是菱形,
∴AB=AD,
又∵四边形ADEF是菱形,
∴AF=AD,
∴AB=AF,
∵∠BAD=∠FAD,
∴AD⊥BF.
(2)解:∵四边形ABCD、ADEF都是菱形,
∴AB=BC=AF,
∵BF=BC,
∴AB=AF= BF,
∴△ABF是等边三角形,
∴∠BAF=60°,
∵∠BAD=∠FAD,
∴∠BAD=30°,
∵四边形ABCD是菱形,
∴AB//CD,
∴∠BAD+∠ADC=180°,
∴∠ADC=150°.
【解析】(1)由菱形的性质得AB=AD,AF=AD,等量代换得AB=AF,又∠BAD=∠FAD,根据等腰三角形三线合一的性质得AD⊥BF.
(2)由菱形的性质得AB=BC=AF,又BF=BC,等量代换得AB=AF= BF,由等边三角形的判定知△ABF是等边三角形,根据等边三角形和菱形的性质得
∠BAD=30°,由菱形和平行线的性质得∠ADC=150°.
【考点精析】利用等腰三角形的性质和菱形的性质对题目进行判断即可得到答案,需要熟知等腰三角形的两个底角相等(简称:等边对等角);菱形的四条边都相等;菱形的对角线互相垂直,并且每一条对角线平分一组对角;菱形被两条对角线分成四个全等的直角三角形;菱形的面积等于两条对角线长的积的一半.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知
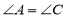 ,
,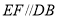 .说明
.说明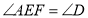 的理由.
的理由.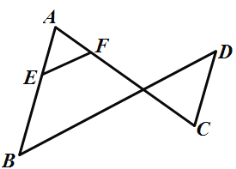
解:∵
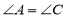 (已知),
(已知),∴________//________(_______________)
∴
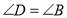 (_______________)
(_______________)∵
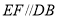 (________),
(________),∴
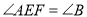 (_______________)
(_______________)∵
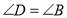 (己证),
(己证),∴
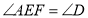 (_______________).
(_______________). -
科目: 来源: 题型:
查看答案和解析>>【题目】一个不透明的口袋内装有四张完全相同的卡片,分别标有数字1、2、3、4。
(1)若任取一张卡片,上面所标数字是不小于3的概率为;
(2)在口袋中任取两张卡片:请你利用树状图或列表法求出这两张卡片上的数字的积为奇数的概率。 -
科目: 来源: 题型:
查看答案和解析>>【题目】(3分)如图,AD是△ABC的角平分线,DE⊥AC,垂足为E,BF∥AC交ED的延长线于点F,若BC恰好平分∠ABF,AE=2BF.给出下列四个结论:①DE=DF;②DB=DC;③AD⊥BC;④AC=3BF,其中正确的结论共有( )

A. 4个 B. 3个 C. 2个 D. 1个
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,O是直线AB上一点,OC为任意一条射线,OD平分∠BOC,OE平分∠AOC.

(1)指出图中∠AOD与∠BOE的补角;
(2)试判断∠COD与∠COE具有怎样的数量关系.并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,在△ABC中,D是AC上一点,E是AB上一点,且∠AED=∠C.
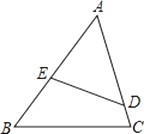
(1)求证:△AED∽△ACB;
(2)若AB=6,AD=4,AC=5,求AE的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,∠A=36°,BD平分∠ABC交AC于点D.求证:AD=BC
证明:∵AB=AC
∴∠ABC=∠C ( )
∵∠A=36°
又∵∠A+∠ABC+∠C=180° ( )
∴∠ABC= °
∵BD平分∠ABC
∴∠1=∠2= °
∴∠C=∠ =72°
∴AD= ,BC= ( )
∴AD=BC

相关试题

