【题目】在平面直角坐标系中,对于点P(x,y),我们把点P′(﹣y+1,x+1)叫作点P的伴随点.已知点A1的伴随点为A2 , 点A2的伴随点为A3 , 点A3的伴随点为A4 , 这样依次得到点A1 , A2 , A3 , A4…,若点A1的坐标为(a,b),对于任意的正整数n,点An均在x轴上方,则a,b应满足的条件为 .
参考答案:
【答案】﹣1<a<1,0<b<2
【解析】解:∵A1的坐标为(4,5),
∴A2(﹣4,5),A3(﹣4,﹣3),A4(4,﹣3),A5(4,5),
…,
依此类推,每4个点为一个循环组依次循环,
∵点A1的坐标为(a,b),
∴A2(﹣b+1,a+1),A3(﹣a,﹣b+2),A4(b﹣1,﹣a+1),A5(a,b),
…,
依此类推,每4个点为一个循环组依次循环,
∵对于任意的正整数n,点An均在x轴上方,
∴ ![]() ,
,
![]() ,
,
解得﹣1<a<1,0<b<2.
所以答案是:﹣1<a<1,0<b<2.
【考点精析】通过灵活运用数与式的规律,掌握先从图形上寻找规律,然后验证规律,应用规律,即数形结合寻找规律即可以解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】“宜居襄阳”是我们的共同愿景,空气质量备受人们关注.我市某空气质量监测站点检测了该区域每天的空气质量情况,统计了2013年1月份至4月份若干天的空气质量情况,并绘制了如下两幅不完整的统计图.

请根据图中信息,解答下列问题:
(1)统计图共统计了 天的空气质量情况;
(2)请将条形统计图补充完整;空气质量为“优”所在扇形的圆心角度数是 ;
(3)从小源所在环保兴趣小组4名同学(2名男同学,2名女同学)中,随机选取两名同学去该空气质量监测站点参观,则恰好选到一名男同学和一名女同学的概率是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图(1),直线
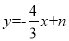 交x轴于点A,交
交x轴于点A,交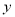 轴于点C(0,4),抛物线
轴于点C(0,4),抛物线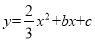 过点A,交y轴于点B(0,-2).点P为抛物线上一个动点,过点P作x轴的垂线PD,过点B作BD⊥PD于点D,连接PB,设点P的横坐标为
过点A,交y轴于点B(0,-2).点P为抛物线上一个动点,过点P作x轴的垂线PD,过点B作BD⊥PD于点D,连接PB,设点P的横坐标为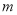 .
.(1)求抛物线的解析式;
(2)当△BDP为等腰直角三角形时,求线段PD的长;
(3)如图(2),将△BDP绕点B 逆时针旋转,得到△BD′P′,当旋转角∠PBP′=∠OAC,且点P的对应点P′落在坐标轴上时,请直接写出点P的坐标.
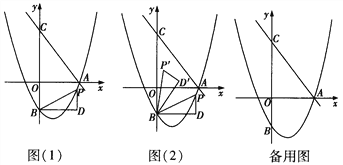
-
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,三边长为9、10、x,则x的取值范围是( )
A. 1≤x<19 B. 1<x≤19 C. 1<x<19 D. 1≤x≤19
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知AB∥DE,∠B=60°,AE⊥BC,垂足为点E.
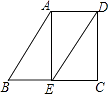
(1)求∠AED的度数;
(2)当∠EDC满足什么条件时,AE∥DC证明你的结论. -
科目: 来源: 题型:
查看答案和解析>>【题目】某公司生产的某种时令商品每件成本为20元, 经过市场调研发现,这种商品在未来40天内的日销售量
 (件)与时间 (天)的关系如下表:
(件)与时间 (天)的关系如下表:时间/天
1
3
6
10
36
…
日销售量
 /件
/件94
90
84
76
24
…
未来40天内,前20天每天的价格
 (元/件)与时间 (天)的函数关系式为
(元/件)与时间 (天)的函数关系式为
(1≤≤20且为整数),后20天每天的价格
 (元/件)与时间(天)的函数关系式
(元/件)与时间(天)的函数关系式 (21≤≤40且为整数).
(21≤≤40且为整数).下面我们就来研究销售这种商品的有关问题:
(1)认真分析上表中的数据,用所学过的一次函数、二次函数、反比例函数的知识确定一个满足这些数据的
 (件)与(天)之间的关系式;
(件)与(天)之间的关系式;(2)请预测未来40天中哪一天的日销售利润最大,最大日销售利润是多少?
(3)在实际销售的前20天中,该公司决定每销售一件商品,就捐赠
 元利润(
元利润( <4)给希望工程.公司通过销售记录发现,前20天中,每天扣除捐赠后的日销售利润随时间(天)的增大而增大,请直接写出
<4)给希望工程.公司通过销售记录发现,前20天中,每天扣除捐赠后的日销售利润随时间(天)的增大而增大,请直接写出 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知线段a=2cm,b=8cm,它们的比例中项c是( )
A.16cmB.4cmC.±4cmD.±16cm
相关试题

