【题目】观察下列各式:
13=![]() ×12×22
×12×22
13+23=9=![]() ×22×32
×22×32
13+23+33=36=![]() ×32×42
×32×42
13+23+33+43=100=![]() ×42×52
×42×52
回答下面的问题:
(1)猜想:13+23+33+…+(n-1)3+ n3=________.
(2)利用你得到的(1)中的结论,计算13+23+33+…+993+1003的值.
(3)计算:213+223+…+993+1003的值.
参考答案:
【答案】(1)![]() n2(n+1)2(2) 25502500;(3) 25458400.
n2(n+1)2(2) 25502500;(3) 25458400.
【解析】
(1)(2)观察已知的等式,发现:等式的左边是连续自然数的立方和,等式的右边是连续自然数的和的平方;由此得出答案即可;
(3)根据(1)中发现的结论,即可求得结论.
(1)∵13=![]() ×12×22
×12×22
13+23=9=![]() ×22×32
×22×32
13+23+33=36=![]() ×32×42
×32×42
13+23+33+43=100=![]() ×42×52
×42×52
…
∴猜想:13+23+33+…+(n-1)3+ n3=![]() n2(n+1)2;
n2(n+1)2;
故填:![]() n2(n+1)2
n2(n+1)2
(2) 13+23+33+…+993+1003=![]() ×1002×1012=25502500;
×1002×1012=25502500;
(3) 213+223+…+993+1003
=13+23+33+…+993+1003(13+23+33+43+…203)
= ![]() ×1002×1012
×1002×1012![]() ×202×212
×202×212
=25458400.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某花卉种植基地准备围建一个面积为100平方米的矩形苗圃园种植玫瑰花,其中一边靠墙,另外三边用29米长的篱笆围成.已知墙长为18米,为方便进入,在墙的对面留出1米宽的门(如图所示),求这个苗圃园垂直于墙的一边长为多少米?

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示的方格纸中,每小方格的边长都为1.请在方格纸上画图并回容问题:已知点A、B.
(1)画直线AB,射线BC;
(2)过点C作垂线段CD⊥AB,垂足为点D.
(3)连结AC,则△ABC的面积=_______.
(4)已知AB=5,求线段CD的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在菱形ABCF中,∠ABC=60°,延长BA至点D,延长CB至点E,使BE=AD,连结CD,EA,延长EA交CD于点G.
(1)求证:△ACE≌△CBD;
(2)求∠CGE的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某化工车间发生有害气体泄漏,自泄漏开始到完全控制利用了40min,之后将对泄漏有害气体进行清理,线段DE表示气体泄漏时车间内危险检测表显示数据y与时间x(min)之间的函数关系(0≤x≤40),反比例函数y=
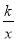 对应曲线EF表示气体泄漏控制之后车间危险检测表显示数据y与时间x(min)之间的函数关系(40≤x≤?).根据图象解答下列问题:
对应曲线EF表示气体泄漏控制之后车间危险检测表显示数据y与时间x(min)之间的函数关系(40≤x≤?).根据图象解答下列问题:(1)危险检测表在气体泄漏之初显示的数据是 ;
(2)求反比例函数y=
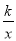 的表达式,并确定车间内危险检测表恢复到气体泄漏之初数据时对应x的值.
的表达式,并确定车间内危险检测表恢复到气体泄漏之初数据时对应x的值.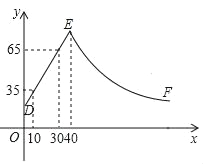
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:在△ABC中,CD⊥AB,∠DEB=∠ACB,∠1+∠2=180°,试判断FG与AB的位置关系,并说明理由.请在下划线内补全解题过程或依据.

解:FG⊥AB,理由如下:
∵∠DEB=∠ACB (已知)
∴AC∥________ (__________________)
∴∠1=∠3(_______________________)
∵∠1+∠2=180°(已知)
∴∠3+∠2=_________(等量代换)
∴FG∥________ (_________________)
∴∠FGA=∠________(_____________)
∵CD⊥AB(已知)
∴∠CDA=90°
∴∠________=90°(等量代换)
∴FG⊥AB(_____________________)
-
科目: 来源: 题型:
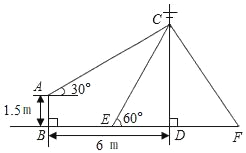
查看答案和解析>>【题目】如图,在电线杆CD上的C处引拉线CE、CF固定电线杆,拉线CE和地面所成的角∠CED=60°,在离电线杆6m的B处安置高为1.5m的测角仪AB,在A处测得电线杆上C处的仰角为30°,求拉线CE的长.(结果保留根号)
相关试题

