搜索
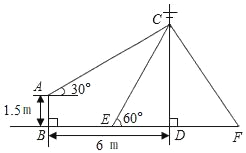
【题目】如图，在电线杆CD上的C处引拉线CE、CF固定电线杆，拉线CE和地面所成的角∠CED=60°，在离电线杆6m的B处安置高为1.5m的测角仪AB，在A处测得电线杆上C处的仰角为30°，求拉线CE的长．（结果保留根号）
参考答案：
【答案】拉线CE的长约为5.7米
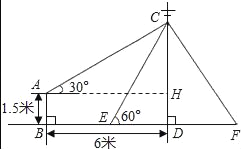
【解析】试题分析：过点A作AH⊥CD，垂足为H，在Rt△ACH中,可求出CH，进而
再在Rt△CDE中，求出
的长．
试题解析：过点A作AH⊥CD，垂足为H，
由题意可知四边形ABDH为矩形, 
∴AB=DH=1.5，BD=AH=6，
在Rt△ACH中, 
∴CH=AHtan∠CAH，
∴
(米)，
∵DH=1.5，
∴
在Rt△CDE中，
∵
∴
(米)，
答：拉线CE的长约为5.7米，
答：拉线CE的长约为5.7米．
-
科目： 来源： 题型：
查看答案和解析>>【题目】观察下列各式：
13＝
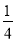×12×2213+23＝9＝
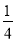×22×3213+23+33＝36＝
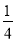×32×4213+23+33+43＝100＝
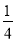×42×52回答下面的问题：
(1)猜想：13+23+33+…+(n－1)3+ n3＝________.
(2)利用你得到的(1)中的结论，计算13+23+33+…+993+1003的值.
(3)计算：213+223+…+993+1003的值.
-
科目： 来源： 题型：
查看答案和解析>>【题目】某化工车间发生有害气体泄漏，自泄漏开始到完全控制利用了40min，之后将对泄漏有害气体进行清理，线段DE表示气体泄漏时车间内危险检测表显示数据y与时间x（min）之间的函数关系（0≤x≤40），反比例函数y=
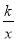对应曲线EF表示气体泄漏控制之后车间危险检测表显示数据y与时间x（min）之间的函数关系（40≤x≤？）．根据图象解答下列问题：（1）危险检测表在气体泄漏之初显示的数据是 ；
（2）求反比例函数y=
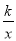的表达式，并确定车间内危险检测表恢复到气体泄漏之初数据时对应x的值．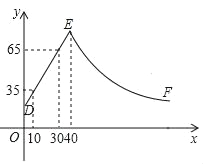
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知：在△ABC中，CD⊥AB，∠DEB=∠ACB，∠1+∠2=180°，试判断FG与AB的位置关系，并说明理由.请在下划线内补全解题过程或依据.
解：FG⊥AB，理由如下：
∵∠DEB=∠ACB (已知)
∴AC∥________ (__________________)
∴∠1=∠3(_______________________)
∵∠1+∠2=180°(已知)
∴∠3+∠2=_________(等量代换)
∴FG∥________ (_________________)
∴∠FGA=∠________(_____________)
∵CD⊥AB(已知)
∴∠CDA=90°
∴∠________=90°(等量代换)
∴FG⊥AB(_____________________)
-
科目： 来源： 题型：
查看答案和解析>>【题目】在Rt△ABC中，AB=BC=5，∠B=90°，将一块等腰直角三角板的直角顶点O放在斜边AC上，三角板的两直角边分别交直线AB、BC于E、F两点．
（1）如图①，若O为AC的中点，点E、F分别在边AB、BC上．
①当△OFC是等腰直角三角形时，∠FOC= ；
②求证：OE=OF；
（2）如图②，若AO：AC=1：4时，OE和OF有怎样的数量关系？证明你发现的结论．
-
科目： 来源： 题型：
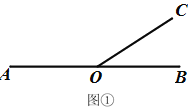
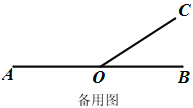
查看答案和解析>>【题目】已知：如图1，点O是直线AB上一点，过点O作射线OC.
(1)若∠AOC=140°，则∠BOC=________°.
(2)在图1中分别画∠AOC的角平分线OE和∠BOC的角平分线OF，那么,OE和OF有什么位置关系，请说明理由.
(3)若∠BOC=30°，射线OD从OB出发，绕点O以每秒10°角的速度逆时针旋转.当射线OD与射线OA重合时，射线OC以每秒30°角的速度绕点O逆时针旋转，射线OD按原来的速度和方向继续旋转，当射线OC或射线OD中有一条射线与射线OB重合时，两条射线都停止.设射线OD旋转的时间为t秒，在旋转的过程中，是否存在某个时刻，使得射线OB、OC与OD中的某一条射线是另两条射线所夹角的平分线?若存在，直接写出所有满足条件的t的值，若不存在，说明理由.
-
科目： 来源： 题型：
查看答案和解析>>【题目】为进一步推进青少年毒品预防教育“627“工程，切实提高广大青少年识毒、防毒、拒毒的意识和能力，我市高度重视全国青少年禁毒知识竞赛活动．针对某校七年级学生的知识竞赛成绩绘制了如图不完整的统计图表．
知识竞赛成绩频数分布表
组别
成绩(分数)
人数
A
95≤x<100
300
B
90≤x<95
a
C
85≤x<90
150
D
80≤x<85
200
E
75≤x<80
b
根据所给信息，解答下列问题．
(1)a＝____，b＝____．
(2)请求出C组所在扇形统计图中的圆心角的度数．
(3)补全知识竞赛成绩频数分布直方图．
(4)已知我市七年级有180000名学生，请估算全市七年级知识竞赛成绩低于80分的人数．
相关试题
