【题目】如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于D,CE平分∠ACD交AB于E,若AC=2,AE=1,则BC=______.

参考答案:
【答案】1.5
【解析】
根据余角的性质得到∠BCD=∠A.根据角平分线的定义得到∠ACE=∠DCE.根据三角形的外角的性质得到∠BEC=∠BCE,求得BC=BE,设BC=BE=x,根据勾股定理列方程即可得到结论.
解:∵∠ACB=90°,CD⊥AB,
∴∠ACD+∠BCD=90°,∠ACD+∠A=90°,
∴∠BCD=∠A.
∵CE平分∠ACD,
∴∠ACE=∠DCE.
又∵∠BEC=∠A+∠ACE,∠BCE=∠BCD+∠DCE,
∴∠BEC=∠BCE,
∴BC=BE,
设BC=BE=x,
∴AB=1+x,
∵AC2+BC2=AB2,
∴22+x2=(1+x)2,
解得:x=1.5,
故答案为:1.5.
-
科目: 来源: 题型:
查看答案和解析>>【题目】平面直角坐标系xOy中,有点P(a,b),实数a,b,m满足以下两个等式:
2a﹣3m+1=0,3b﹣2m﹣16=0
(1)当a=1时,点P到x轴的距离为 ;
(2)若点P落在x轴上,点P平移后对应点为P′(a+15,b+4),求点P和P′的坐标;
(3)当a≤4<b时,求m的最小整数值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x的一元二次方程x2+(m+2)x+m=0,
(1)求证:无论m取何值,原方程总有两个不相等的实数根.
(2)若x1 , x2是原方程的两根,且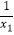 +
+  =﹣2,求m的值.
=﹣2,求m的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=3cm、AC=4cm、BC=5cm,在△ABC所在平面内画一条直线,将△ABC分割成两个三角形,使其中的一个是等腰三角形,则这样的直线最多可画的条数为( )

A. 3B. 4C. 5D. 6
-
科目: 来源: 题型:
查看答案和解析>>【题目】李老师为了了解所教班级学生完成数学课前预习的具体情况,对本班部分学生进行了为期半个月的跟踪调查,他将调查结果分为四类,A:很好;B:较好;C:一般;D:较差.并将调查结果绘制成以下两幅不完整的统计图,请你根据统计图解答下列问题:
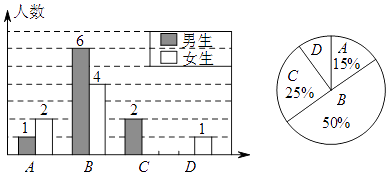
(1)若D类男生有1名,请计算出C类女生的人数,并将条形统计图补充完整.
(2)为了共同进步,李老师想从被调查的A类和D类学生中各随机选取一位同学进行“一帮一”互助学习,请用列表法或画树形图的方法求出所选两位同学恰好是两位男同学的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】新冠肺炎疫情期间,某口罩厂为生产更多的口罩满足疫情防控需求,决定拨款456万元购进A,B两种型号的口罩机共30台.两种型号口罩机的单价和工作效率分别如下表:
单价/万元
工作效率/(只/h)
A种型号
16
4000
B种型号
14.8
3000
(1)求购进A,B两种型号的口罩生产线各多少台.
(2)现有200万只口罩的生产任务,计划安排新购进的口罩机共15台同时进行生产.若工厂的工人每天工作8h,则至少租用A种型号的口罩机多少台才能在5天内完成任务?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知点A(2m-1,4m+2015)、B(-
 n+
n+ ,-n+2020)在直线y=kx+b上,则k+b值为______.
,-n+2020)在直线y=kx+b上,则k+b值为______.
相关试题

