【题目】已知关于x的一元二次方程x2+(m+2)x+m=0,
(1)求证:无论m取何值,原方程总有两个不相等的实数根.
(2)若x1 , x2是原方程的两根,且 ![]() +
+ ![]() =﹣2,求m的值.
=﹣2,求m的值.
参考答案:
【答案】
(1)解:证明:△=(m+2)2﹣4m=m2+4.
∵m2≥0,
∴m2+4>0,即△>0,
∴无论m取何值,原方程总有两个不相等的实数根.
(2)解:∵x1,x2是原方程的两根,
∴x1+x2=﹣(m+2),x1x2=m.
∵ ![]() +
+ ![]() =
= ![]() =﹣
=﹣ ![]() =﹣2,
=﹣2,
解得:m=2,
经检验,m=2是分式方程的解,且符合题意,
∴m的值为2.
【解析】由△=(m+2)2﹣4m=m2+4知m2+4>0,即△>0,故无论m取何值,原方程总有两个不相等的实数根;(2)根据根与系数的关系得∴x1+x2=﹣(m+2),x1x2=m,再将分式方程的左边变形 ,整体代入即可。
【考点精析】本题主要考查了求根公式和根与系数的关系的相关知识点,需要掌握根的判别式△=b2-4ac,这里可以分为3种情况:1、当△>0时,一元二次方程有2个不相等的实数根2、当△=0时,一元二次方程有2个相同的实数根3、当△<0时,一元二次方程没有实数根;一元二次方程ax2+bx+c=0(a≠0)的根由方程的系数a、b、c而定;两根之和等于方程的一次项系数除以二次项系数所得的商的相反数;两根之积等于常数项除以二次项系数所得的商才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,四边形ABED是正方形,DB⊥BC,点E为线段DC的中点,
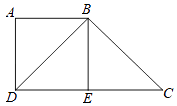
(1)求证:BD2=ADDC.
(2)连接AE,求证:ABCE为平行四边形. -
科目: 来源: 题型:
查看答案和解析>>【题目】填空完成推理过程:
如图,BCE,AFE是直线,AB∥CD,∠1=∠2,∠3=∠4,求证AD∥BE.

证明:∵AB∥CD(已知)
∴∠4=∠BAE( )
∵∠3=∠4(已知)
∴∠3=∠ (等量代换)
∵∠1=∠2(已知)
∴∠1+∠CAF=∠2+∠CAF( )
即∠BAF=∠CAD
∴∠3=∠ (等量代换)
∴AD∥BE( )
-
科目: 来源: 题型:
查看答案和解析>>【题目】平面直角坐标系xOy中,有点P(a,b),实数a,b,m满足以下两个等式:
2a﹣3m+1=0,3b﹣2m﹣16=0
(1)当a=1时,点P到x轴的距离为 ;
(2)若点P落在x轴上,点P平移后对应点为P′(a+15,b+4),求点P和P′的坐标;
(3)当a≤4<b时,求m的最小整数值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=3cm、AC=4cm、BC=5cm,在△ABC所在平面内画一条直线,将△ABC分割成两个三角形,使其中的一个是等腰三角形,则这样的直线最多可画的条数为( )

A. 3B. 4C. 5D. 6
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于D,CE平分∠ACD交AB于E,若AC=2,AE=1,则BC=______.

-
科目: 来源: 题型:
查看答案和解析>>【题目】李老师为了了解所教班级学生完成数学课前预习的具体情况,对本班部分学生进行了为期半个月的跟踪调查,他将调查结果分为四类,A:很好;B:较好;C:一般;D:较差.并将调查结果绘制成以下两幅不完整的统计图,请你根据统计图解答下列问题:
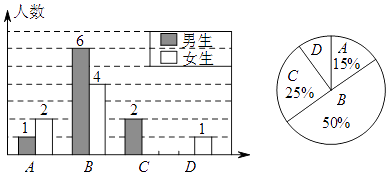
(1)若D类男生有1名,请计算出C类女生的人数,并将条形统计图补充完整.
(2)为了共同进步,李老师想从被调查的A类和D类学生中各随机选取一位同学进行“一帮一”互助学习,请用列表法或画树形图的方法求出所选两位同学恰好是两位男同学的概率.
相关试题

