【题目】平面直角坐标系xOy中,有点P(a,b),实数a,b,m满足以下两个等式:
2a﹣3m+1=0,3b﹣2m﹣16=0
(1)当a=1时,点P到x轴的距离为 ;
(2)若点P落在x轴上,点P平移后对应点为P′(a+15,b+4),求点P和P′的坐标;
(3)当a≤4<b时,求m的最小整数值.
参考答案:
【答案】(1)6;(2)点P的坐标是![]() ,点
,点![]() 的坐标是
的坐标是![]() ;(3)-1.
;(3)-1.
【解析】
(1)把a=1分别代入2a﹣3m+1=0,3b﹣2m﹣16=0就可求出P点的坐标,点P到x轴的距离就是P点的纵坐标的绝对值;
(2)由点P落在x轴上可知,b=0,分别代入3b﹣2m﹣16=0,2a﹣3m+1=0可求出点P的坐标,再代入P′(a+15,b+4)中,即可求出点P′的坐标;
(3)a,b分别用m表示,根据a≤4<b建立关于m的不等式组,解不等式组即可求出答案.
(1)∵a=1,2a﹣3m+1=0,
∴2-3m+1=0,
∴m=1,
∵3b﹣2m﹣16=0,
∴3b-2-16=0
∴b=6,
∴P的坐标为(1,6),
∴点P到x轴的距离是6,
故答案为:6.
(2)∵点P落在x轴上,
∴b=0,
∴3![]() 0-2m-16=0,
0-2m-16=0,
∴m=-8,
∴2a-3![]() (-8)+1=0,
(-8)+1=0,
∴![]() ,
,
∴![]() ,
,![]() ,
,
∴点P的坐标是![]() ,点
,点![]() 的坐标是
的坐标是![]() ;
;
(3)∵2a-3m+1=0,
∴![]() ,
,
∵3b-2m-16=0,
∴![]() ,且
,且![]() ,
,
∴![]() ,
,
解不等式组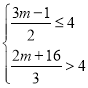 ,
,
∴解得:![]() ,
,
∴m的最小整数值是-1.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算
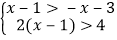
(1)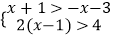
(2)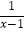 +1=
+1= 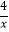 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,四边形ABED是正方形,DB⊥BC,点E为线段DC的中点,
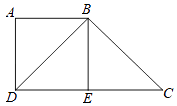
(1)求证:BD2=ADDC.
(2)连接AE,求证:ABCE为平行四边形. -
科目: 来源: 题型:
查看答案和解析>>【题目】填空完成推理过程:
如图,BCE,AFE是直线,AB∥CD,∠1=∠2,∠3=∠4,求证AD∥BE.

证明:∵AB∥CD(已知)
∴∠4=∠BAE( )
∵∠3=∠4(已知)
∴∠3=∠ (等量代换)
∵∠1=∠2(已知)
∴∠1+∠CAF=∠2+∠CAF( )
即∠BAF=∠CAD
∴∠3=∠ (等量代换)
∴AD∥BE( )
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x的一元二次方程x2+(m+2)x+m=0,
(1)求证:无论m取何值,原方程总有两个不相等的实数根.
(2)若x1 , x2是原方程的两根,且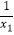 +
+  =﹣2,求m的值.
=﹣2,求m的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=3cm、AC=4cm、BC=5cm,在△ABC所在平面内画一条直线,将△ABC分割成两个三角形,使其中的一个是等腰三角形,则这样的直线最多可画的条数为( )

A. 3B. 4C. 5D. 6
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于D,CE平分∠ACD交AB于E,若AC=2,AE=1,则BC=______.

相关试题

