【题目】如图,已知AB∥CD,点E、F分别在直线AB、CD上,∠EPF=90°,∠BEP=∠GEP,则∠1与∠2的数量关系为( )
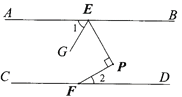
A. ∠1=∠2B. ∠1=2∠2C. ∠1=3∠2D. ∠1=4∠2
参考答案:
【答案】B
【解析】
延长EP交CD于点M,由三角形外角的性质可得∠FMP=90°-∠2,再根据平行线的性质可得∠BEP=∠FMP,继而根据平角定义以及∠BEP=∠GEP即可求得答案.
延长EP交CD于点M,
∵∠EPF是△FPM的外角,
∴∠2+∠FMP=∠EPF=90°,
∴∠FMP=90°-∠2,
∵AB//CD,
∴∠BEP=∠FMP,
∴∠BEP=90°-∠2,
∵∠1+∠BEP+∠GEP=180°,∠BEP=∠GEP,
∴∠1+90°-∠2+90°-∠2=180°,
∴∠1=2∠2,
故选B.

-
科目: 来源: 题型:
查看答案和解析>>【题目】小林在某商店购买商品A、B共三次,只有一次购买时,商品A、B同时打折(折扣相同),其余两次均按标价购买.三次购买商品A、B的数量和费用如下表:
购买商品A的数量/个
购买商品B的数量/个
购买总费用/元
第一次购物
6
5
1140
第二次购物
3
7
1110
第三次购物
9
8
1062
(1)小林以折扣价购买商品A、B是第 次购物;
(2)求出商品A、B的标价;
(3)若商品A、B的折扣相同,问商店是打几折出售这两种商品的?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在
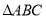 中,点
中,点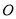 是
是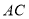 边上的一个动点,过点
边上的一个动点,过点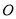 作直线
作直线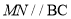 ,设
,设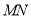 交
交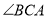 的角平分线于点
的角平分线于点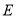 ,交
,交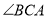 的外角平分线于点
的外角平分线于点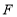 .
.(1)求证:
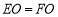 ;
;(2)当点
 运动到何处时,四边形
运动到何处时,四边形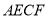 是矩形?并证明你的结论.
是矩形?并证明你的结论.(3)当点
 运动到何处,且
运动到何处,且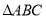 满足什么条件时,四边形
满足什么条件时,四边形 是正方形?并说明理由.
是正方形?并说明理由.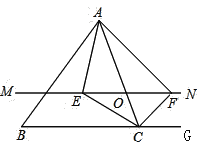
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,长方形ABCD在平面直角坐标系中,AD∥BC∥x轴,AB∥DC∥y轴,x轴与y轴夹角为90°,点M,N分别在xy轴上,点A(1,8),B(1,6),C(7,6),D(7,8).

(1)连接线段OB、OD、BD,求△OBD的面积;
(2)若长方形ABCD在第一象限内以每秒0.5个单位长度的速度向下平移,经过多少秒时,△OBD的面积与长方形ABCD的面积相等请直接写出答案;
(3)见备用图,连接 OB,OD,OD交BC于点E,∠BON的平分线和∠BEO的平分线交于点F.
①当∠BEO的度数为n,∠BON的度数为m时,求∠OFE的度数.
②请直接写出∠OFE和∠BOE之间的数量关系.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,平面直角坐标系中,
 ,
, ,
, ,
, ,直线
,直线 过
过 点,且与
点,且与 轴交于
轴交于 点.
点.(1)求点
 、点
、点 的坐标;
的坐标;(2)试说明:
 ;
;(3)若点
 是直线
是直线 上的一个动点,在
上的一个动点,在 轴上是否存在另一个点
轴上是否存在另一个点 ,使以
,使以 、
、 、
、 、
、 为顶点的四边形是平行四边形?若存在,请直接写出点
为顶点的四边形是平行四边形?若存在,请直接写出点 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
 ,A、B分别为直线
,A、B分别为直线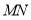 、
、 上两点,且
上两点,且 ,若射线
,若射线 绕点顺时针旋转至
绕点顺时针旋转至 后立即回转,射线
后立即回转,射线 绕点B逆时针旋转至
绕点B逆时针旋转至 后立即回转,两射线分别绕点A、点B不停地旋转,若射线
后立即回转,两射线分别绕点A、点B不停地旋转,若射线 转动的速度是
转动的速度是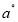 /秒,射线
/秒,射线 转动的速度是
转动的速度是 /秒,且a、b满足
/秒,且a、b满足 .若射线
.若射线 绕点A顺时针先转动18秒,射线
绕点A顺时针先转动18秒,射线 才开始绕点B逆时针旋转,在射线
才开始绕点B逆时针旋转,在射线 到达
到达 之前,问射线
之前,问射线 再转动_______秒时,射线
再转动_______秒时,射线 与射线
与射线 互相平行.
互相平行.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)如图1,在四边形
 中,
中, ,
, 、
、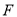 分别是
分别是 、
、 的中点,连接
的中点,连接 并延长,分别与
并延长,分别与 、
、 的延长线交于点
的延长线交于点 、
、 ,证明:
,证明: .
.请将证明
 的过程填写完整:
的过程填写完整:证明:连接
 ,取
,取 的中点
的中点 ,连接
,连接 、
、 .
. 是
是 的中点,
的中点, 是
是 的中点,
的中点,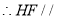 ________,
________, _______,同理:
_______,同理: _______,
_______, _______,
_______, ,
,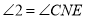 ,
,又
 ,
, ,
,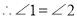 ,
, .
.(2)运用上题方法解决下列问题:
问题一:如图2,在四边形
 中,
中, 与
与 相交于点
相交于点 ,
, ,
, 、
、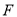 分别是
分别是 、
、 的中点,连接
的中点,连接 ,分别交
,分别交 、
、 于点
于点 、
、 ,请判断
,请判断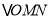 的形状,并说明理由;
的形状,并说明理由;问题二:如图3,在钝角
 中,
中, ,
, 点在
点在 上,
上, 、
、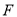 分别是
分别是 、
、 的中点,连接
的中点,连接 并延长,与
并延长,与 的延长线交于点
的延长线交于点 ,连接
,连接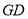 ,若
,若 ,
, 是直角三角形且
是直角三角形且 ,求证:
,求证: .
.


相关试题

