【题目】如图,![]() ,A、B分别为直线
,A、B分别为直线![]() 、
、![]() 上两点,且
上两点,且![]() ,若射线
,若射线![]() 绕点顺时针旋转至
绕点顺时针旋转至![]() 后立即回转,射线
后立即回转,射线![]() 绕点B逆时针旋转至
绕点B逆时针旋转至![]() 后立即回转,两射线分别绕点A、点B不停地旋转,若射线
后立即回转,两射线分别绕点A、点B不停地旋转,若射线![]() 转动的速度是
转动的速度是![]() /秒,射线
/秒,射线![]() 转动的速度是
转动的速度是![]() /秒,且a、b满足
/秒,且a、b满足![]() .若射线
.若射线![]() 绕点A顺时针先转动18秒,射线
绕点A顺时针先转动18秒,射线![]() 才开始绕点B逆时针旋转,在射线
才开始绕点B逆时针旋转,在射线![]() 到达
到达![]() 之前,问射线
之前,问射线![]() 再转动_______秒时,射线
再转动_______秒时,射线![]() 与射线
与射线![]() 互相平行.
互相平行.

参考答案:
【答案】15或22.5
【解析】
先由题意得出a,b的值,再推出射线AM绕点A顺时针先转动18秒后,AM转动至AM![]() 的位置,∠MAM
的位置,∠MAM![]() =18°×5=90°,然后分情况讨论即可.
=18°×5=90°,然后分情况讨论即可.
∵![]() ,
,
∴a=5,b=1,
设射线AM再转动t秒时,射线AM、射线BQ互相平行,如图,射线AM绕点A顺时针先转动18秒后,AM转动至AM![]() 的位置,∠MAM
的位置,∠MAM![]() =18°×5=90°,分两种情况:
=18°×5=90°,分两种情况:

①当9<t<18时,如图,∠QBQ![]() =t°,∠M
=t°,∠M![]() AM"=5t°,
AM"=5t°,
∵∠BAN=45°=∠ABQ,
∴∠ABQ![]() =45°-t°,∠BAM"=5t-45°,
=45°-t°,∠BAM"=5t-45°,
当∠ABQ![]() =∠BAM"时,BQ
=∠BAM"时,BQ![]() //AM",
//AM",
此时,45°-t°=5t-45°,
解得t=15;

②当18<t<27时,如图∠QBQ![]() =t°,∠NAM"=5t°-90°,
=t°,∠NAM"=5t°-90°,
∵∠BAN=45°=∠ABQ,
∴∠ABQ![]() =45°-t°,∠BAM"=45°-(5t°-90°)=135°-5t°,
=45°-t°,∠BAM"=45°-(5t°-90°)=135°-5t°,
当∠ABQ![]() =∠BAM"时,BQ
=∠BAM"时,BQ![]() //AM",
//AM",
此时,45°-t°=135°-5t,
解得t=22.5;
综上所述,射线AM再转动15秒或22.5秒时,射线AM射线BQ互相平行.
故答案为:15或22.5
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,长方形ABCD在平面直角坐标系中,AD∥BC∥x轴,AB∥DC∥y轴,x轴与y轴夹角为90°,点M,N分别在xy轴上,点A(1,8),B(1,6),C(7,6),D(7,8).

(1)连接线段OB、OD、BD,求△OBD的面积;
(2)若长方形ABCD在第一象限内以每秒0.5个单位长度的速度向下平移,经过多少秒时,△OBD的面积与长方形ABCD的面积相等请直接写出答案;
(3)见备用图,连接 OB,OD,OD交BC于点E,∠BON的平分线和∠BEO的平分线交于点F.
①当∠BEO的度数为n,∠BON的度数为m时,求∠OFE的度数.
②请直接写出∠OFE和∠BOE之间的数量关系.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知AB∥CD,点E、F分别在直线AB、CD上,∠EPF=90°,∠BEP=∠GEP,则∠1与∠2的数量关系为( )
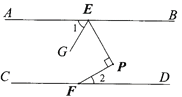
A. ∠1=∠2B. ∠1=2∠2C. ∠1=3∠2D. ∠1=4∠2
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,平面直角坐标系中,
 ,
, ,
, ,
, ,直线
,直线 过
过 点,且与
点,且与 轴交于
轴交于 点.
点.(1)求点
 、点
、点 的坐标;
的坐标;(2)试说明:
 ;
;(3)若点
 是直线
是直线 上的一个动点,在
上的一个动点,在 轴上是否存在另一个点
轴上是否存在另一个点 ,使以
,使以 、
、 、
、 、
、 为顶点的四边形是平行四边形?若存在,请直接写出点
为顶点的四边形是平行四边形?若存在,请直接写出点 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)如图1,在四边形
 中,
中, ,
, 、
、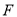 分别是
分别是 、
、 的中点,连接
的中点,连接 并延长,分别与
并延长,分别与 、
、 的延长线交于点
的延长线交于点 、
、 ,证明:
,证明: .
.请将证明
 的过程填写完整:
的过程填写完整:证明:连接
 ,取
,取 的中点
的中点 ,连接
,连接 、
、 .
. 是
是 的中点,
的中点, 是
是 的中点,
的中点,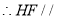 ________,
________, _______,同理:
_______,同理: _______,
_______, _______,
_______, ,
,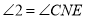 ,
,又
 ,
, ,
,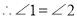 ,
, .
.(2)运用上题方法解决下列问题:
问题一:如图2,在四边形
 中,
中, 与
与 相交于点
相交于点 ,
, ,
, 、
、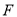 分别是
分别是 、
、 的中点,连接
的中点,连接 ,分别交
,分别交 、
、 于点
于点 、
、 ,请判断
,请判断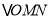 的形状,并说明理由;
的形状,并说明理由;问题二:如图3,在钝角
 中,
中, ,
, 点在
点在 上,
上, 、
、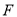 分别是
分别是 、
、 的中点,连接
的中点,连接 并延长,与
并延长,与 的延长线交于点
的延长线交于点 ,连接
,连接 ,若
,若 ,
, 是直角三角形且
是直角三角形且 ,求证:
,求证: .
.


-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,
 ,M是BC的中点,DM平分
,M是BC的中点,DM平分 .
.
(1)求证:AM平分
 ;
; (2)线段DM与AM有怎样的位置关系?请说明理由;
(3)线段CD、AB、AD间有怎样的数量关系?请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图EF∥CD,∠1+∠2=180°.
(1)试说明GD∥CA;
(2)若CD平分∠ACB,DG平分∠CDB,且∠A=40°,求∠ACB的度数.

相关试题

