【题目】(1)如图1,在四边形![]() 中,
中,![]() ,
,![]() 、
、![]() 分别是
分别是![]() 、
、![]() 的中点,连接
的中点,连接![]() 并延长,分别与
并延长,分别与![]() 、
、![]() 的延长线交于点
的延长线交于点![]() 、
、![]() ,证明:
,证明:![]() .
.
请将证明![]() 的过程填写完整:
的过程填写完整:
证明:连接![]() ,取
,取![]() 的中点
的中点![]() ,连接
,连接![]() 、
、![]() .
.
![]() 是
是![]() 的中点,
的中点,![]() 是
是![]() 的中点,
的中点,
![]() ________,
________,![]() _______,同理:
_______,同理:![]() _______,
_______,![]() _______,
_______,
![]() ,
,![]() ,
,
又![]() ,
,![]() ,
,![]() ,
,![]() .
.
(2)运用上题方法解决下列问题:
问题一:如图2,在四边形![]() 中,
中,![]() 与
与![]() 相交于点
相交于点![]() ,
,![]() ,
,![]() 、
、![]() 分别是
分别是![]() 、
、![]() 的中点,连接
的中点,连接![]() ,分别交
,分别交![]() 、
、![]() 于点
于点![]() 、
、![]() ,请判断
,请判断![]() 的形状,并说明理由;
的形状,并说明理由;
问题二:如图3,在钝角![]() 中,
中,![]() ,
,![]() 点在
点在![]() 上,
上,![]() 、
、![]() 分别是
分别是![]() 、
、![]() 的中点,连接
的中点,连接![]() 并延长,与
并延长,与![]() 的延长线交于点
的延长线交于点![]() ,连接
,连接![]() ,若
,若![]() ,
,![]() 是直角三角形且
是直角三角形且![]() ,求证:
,求证:![]() .
.



参考答案:
【答案】(1)![]() ;
;![]() ;
;![]() ;
;![]() ;(2)△OMN为等腰三角形,理由见详解;(3)见详解
;(2)△OMN为等腰三角形,理由见详解;(3)见详解
【解析】
(1)根据题目已知条件补充完整即可;
解:(1)证明:连接![]() ,取
,取![]() 的中点
的中点![]() ,连接
,连接![]() 、
、![]() .
.
![]() 是
是![]() 的中点,
的中点,![]() 是
是![]() 的中点,
的中点,
![]() ,
,![]() ,同理:
,同理:![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
又![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
故答案为:![]() ;
;![]() ;
;![]() ;
;![]() ;
;
(2)△OMN为等腰三角形;
证明:取AC中点P,连接PF,PE,

可知PE=![]() ,PE∥AB,
,PE∥AB,
∴∠PEF=∠ANF,
同理PF=![]() ,
,
PF∥CD,
∴∠PFE=∠CME,
又PE=PF,
∴∠PFE=∠PEF,
∴∠OMN=∠ONM,
∴△OMN为等腰三角形;
(3)如图连接BD,取BD的中点H,连接HF、HE,
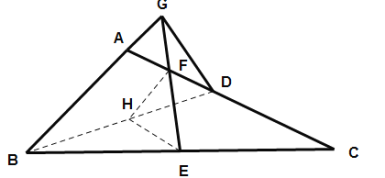
∵F是AD的中点,
∴HF∥AB, HF=![]()
同理,HE∥CD,HE=![]()
∵GF为直角三角形斜边上的中线
∴![]()
∵![]()
∴△AGF是等边三角形
∴∠AGF=∠EFC=∠HFE=60°
∵![]()
∴![]()
∴![]()
∴![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知AB∥CD,点E、F分别在直线AB、CD上,∠EPF=90°,∠BEP=∠GEP,则∠1与∠2的数量关系为( )
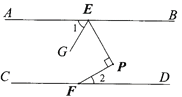
A. ∠1=∠2B. ∠1=2∠2C. ∠1=3∠2D. ∠1=4∠2
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,平面直角坐标系中,
 ,
, ,
, ,
, ,直线
,直线 过
过 点,且与
点,且与 轴交于
轴交于 点.
点.(1)求点
 、点
、点 的坐标;
的坐标;(2)试说明:
 ;
;(3)若点
 是直线
是直线 上的一个动点,在
上的一个动点,在 轴上是否存在另一个点
轴上是否存在另一个点 ,使以
,使以 、
、 、
、 、
、 为顶点的四边形是平行四边形?若存在,请直接写出点
为顶点的四边形是平行四边形?若存在,请直接写出点 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
 ,A、B分别为直线
,A、B分别为直线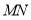 、
、 上两点,且
上两点,且 ,若射线
,若射线 绕点顺时针旋转至
绕点顺时针旋转至 后立即回转,射线
后立即回转,射线 绕点B逆时针旋转至
绕点B逆时针旋转至 后立即回转,两射线分别绕点A、点B不停地旋转,若射线
后立即回转,两射线分别绕点A、点B不停地旋转,若射线 转动的速度是
转动的速度是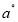 /秒,射线
/秒,射线 转动的速度是
转动的速度是 /秒,且a、b满足
/秒,且a、b满足 .若射线
.若射线 绕点A顺时针先转动18秒,射线
绕点A顺时针先转动18秒,射线 才开始绕点B逆时针旋转,在射线
才开始绕点B逆时针旋转,在射线 到达
到达 之前,问射线
之前,问射线 再转动_______秒时,射线
再转动_______秒时,射线 与射线
与射线 互相平行.
互相平行.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,
 ,M是BC的中点,DM平分
,M是BC的中点,DM平分 .
.
(1)求证:AM平分
 ;
; (2)线段DM与AM有怎样的位置关系?请说明理由;
(3)线段CD、AB、AD间有怎样的数量关系?请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图EF∥CD,∠1+∠2=180°.
(1)试说明GD∥CA;
(2)若CD平分∠ACB,DG平分∠CDB,且∠A=40°,求∠ACB的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读材料:把形如
 的二次三项式(或其一部分)配成完全平方式的方法叫做配方法.配方法的基本形式是完全平方公式的逆写,即
的二次三项式(或其一部分)配成完全平方式的方法叫做配方法.配方法的基本形式是完全平方公式的逆写,即 .例如:
.例如: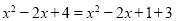
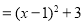 是
是 的一种形式的配方;所以,
的一种形式的配方;所以,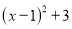 ,
,
 ,
,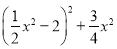 是
是 的三种不同形式的配方(即“余项”分别是常数项、一次项、二次项).
的三种不同形式的配方(即“余项”分别是常数项、一次项、二次项).请根据阅读材料解决下列问题:
(1)比照上面的例子,写出
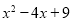 三种不同形式的配方;
三种不同形式的配方;(2)已知
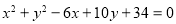 ,求
,求 的值;
的值;(3)已知
 ,求
,求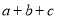 的值.
的值.
相关试题

