【题目】如图,在![]() 中,点
中,点![]() 是
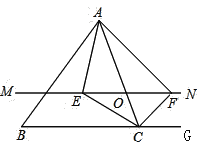
是![]() 边上的一个动点,过点
边上的一个动点,过点![]() 作直线
作直线![]() ,设
,设![]() 交
交![]() 的角平分线于点
的角平分线于点![]() ,交
,交![]() 的外角平分线于点
的外角平分线于点![]() .
.
(1)求证:![]() ;
;
(2)当点![]() 运动到何处时,四边形
运动到何处时,四边形![]() 是矩形?并证明你的结论.
是矩形?并证明你的结论.
(3)当点![]() 运动到何处,且
运动到何处,且![]() 满足什么条件时,四边形
满足什么条件时,四边形![]() 是正方形?并说明理由.
是正方形?并说明理由.
参考答案:
【答案】(1)详见解析;(2)当点![]() 运动到
运动到![]() 的中点时,四边形
的中点时,四边形![]() 是矩形,理由详见解析;(3)当点
是矩形,理由详见解析;(3)当点![]() 运动到
运动到![]() 的中点时,且
的中点时,且![]() 满足
满足![]() 为直角的直角三角形时,四边形
为直角的直角三角形时,四边形![]() 是正方形,理由详见解析.
是正方形,理由详见解析.
【解析】
(1)由平行线的性质和角平分线的定义得出![]() ,
,![]() , 得出
, 得出![]() ,
,![]() ,即可得出结论;
,即可得出结论;
(2)先证明四边形![]() 是平行四边形,再由对角线相等,即可得出结论;
是平行四边形,再由对角线相等,即可得出结论;
(3)由正方形的性质得出![]() ,得出
,得出![]() 即可.
即可.
(1)![]() ,
,
![]() ,
,
又![]() 平分
平分![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
同理:![]() ,
,
![]() .
.

(2)当点![]() 运动到
运动到![]() 的中点时,四边形
的中点时,四边形![]() 是矩形.
是矩形.
![]() 当点
当点![]() 运动到
运动到![]() 的中点时,
的中点时,![]() ,
,
又![]() ,
,
![]() 四边形
四边形![]() 是平行四边形,
是平行四边形,
由(1)可知,![]() ,
,
![]() ,
,
![]() ,即
,即![]() ,
,
![]() 四边形
四边形![]() 是矩形.
是矩形.
(3)当点![]() 运动到
运动到![]() 的中点时,且
的中点时,且![]() 满足
满足![]() 为直角的直角三角形时,四边形
为直角的直角三角形时,四边形![]() 是正方形.
是正方形.
![]() 由(2)知,当点
由(2)知,当点![]() 运动到
运动到![]() 的中点时,四边形
的中点时,四边形![]() 是矩形,
是矩形,
![]() ,
,
![]()
![]() ,
,
![]() ,
,
![]() ,
,
![]() 四边形
四边形![]() 是正方形.
是正方形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】5只不透明的袋子中各装有10个球,每个球除颜色外都相同.
(1)将球搅匀,分别从每只袋子中摸一个球,摸到白球的概率一样大吗?为什么?
(2)将袋子的序号按摸到白球的概率从小到大的顺序排列.





(1) (2) (3) (4) (5)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=﹣
 x2+bx+e与x轴交于点A(﹣3,0)、点B(9,0),与y轴交于点C,顶点为D,连接AD、DB,点P为线段AD上一动点.
x2+bx+e与x轴交于点A(﹣3,0)、点B(9,0),与y轴交于点C,顶点为D,连接AD、DB,点P为线段AD上一动点.
(1)求抛物线的解析式;
(2)如图1,过点P作BD的平行线,交AB于点Q,连接DQ,设AQ=m,△PDQ的面积为S,求S关于m的函数解析式,以及S的最大值;
(3)如图2,抛物线对称轴与x轴交与点G,E为OG的中点,F为点C关于DG对称的对称点,过点P分别作直线EF、DG的垂线,垂足为M、N,连接MN,直接写出△PMN为等腰三角形时点P的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】小林在某商店购买商品A、B共三次,只有一次购买时,商品A、B同时打折(折扣相同),其余两次均按标价购买.三次购买商品A、B的数量和费用如下表:
购买商品A的数量/个
购买商品B的数量/个
购买总费用/元
第一次购物
6
5
1140
第二次购物
3
7
1110
第三次购物
9
8
1062
(1)小林以折扣价购买商品A、B是第 次购物;
(2)求出商品A、B的标价;
(3)若商品A、B的折扣相同,问商店是打几折出售这两种商品的?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,长方形ABCD在平面直角坐标系中,AD∥BC∥x轴,AB∥DC∥y轴,x轴与y轴夹角为90°,点M,N分别在xy轴上,点A(1,8),B(1,6),C(7,6),D(7,8).

(1)连接线段OB、OD、BD,求△OBD的面积;
(2)若长方形ABCD在第一象限内以每秒0.5个单位长度的速度向下平移,经过多少秒时,△OBD的面积与长方形ABCD的面积相等请直接写出答案;
(3)见备用图,连接 OB,OD,OD交BC于点E,∠BON的平分线和∠BEO的平分线交于点F.
①当∠BEO的度数为n,∠BON的度数为m时,求∠OFE的度数.
②请直接写出∠OFE和∠BOE之间的数量关系.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知AB∥CD,点E、F分别在直线AB、CD上,∠EPF=90°,∠BEP=∠GEP,则∠1与∠2的数量关系为( )
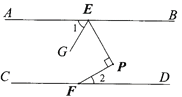
A. ∠1=∠2B. ∠1=2∠2C. ∠1=3∠2D. ∠1=4∠2
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,平面直角坐标系中,
 ,
, ,
, ,
, ,直线
,直线 过
过 点,且与
点,且与 轴交于
轴交于 点.
点.(1)求点
 、点
、点 的坐标;
的坐标;(2)试说明:
 ;
;(3)若点
 是直线
是直线 上的一个动点,在
上的一个动点,在 轴上是否存在另一个点
轴上是否存在另一个点 ,使以
,使以 、
、 、
、 、
、 为顶点的四边形是平行四边形?若存在,请直接写出点
为顶点的四边形是平行四边形?若存在,请直接写出点 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
相关试题

