【题目】如图,在△ABC中,BD平分∠ABC,∠A=2∠C.
(1)若∠C=38°,则∠ABD= ;
(2)求证:BC=AB+AD;
(3)求证:BC2=AB2+ABAC.

参考答案:
【答案】(1)33°;(2)证明见解析.(3)证明见解析.
【解析】试题分析:(1)在BC上截取BE=AB,利用“边角边”证明△ABD和△BED全等,根据全等三角形对应边相等可得DE=AD,全等三角形对应角相等可得∠AED=∠A,然后求出∠C=∠CDE,根据等角对等边可得CE=DE,然后结合图形整理即可得证;
(2)由(1)知:△ABD≌△BED,根据全等三角形对应边相等可得DE=AD,全等三角形对应角相等可得∠AED=∠A,然后求出∠C=∠CDE,根据等角对等边可得CE=DE,等量代换得到EC=AD,即得答案BC=BE+EC=AB+AD;
(3)为了把∠A=2∠C转化成两个角相等的条件,可以构造辅助线:在AC上取BF=BA,连接AE,根据线段的垂直平分线的性质以及三角形的内角和定理的推论能够证明AB=F.再根据勾股定理表示出BC2,AB2.再运用代数中的公式进行计算就可证明.
试题解析:(1)在BC上截取BE=BA,如图1,
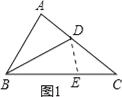
在△ABD和△BED中,
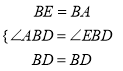 ,
,
∴△ABD≌△BED,
∴∠BED=∠A,
∵∠C=38°,∠A=2∠C,
∴∠A=76°,
∴∠ABC=180°﹣∠C﹣∠A=66°,
BD平分∠ABC,
∴∠ABD=33°;
(2)由(1)知:△ABD≌△BED,
∴BE=AB,DE=AD,∠BED=∠A,
又∵∠A=2∠C,
∴∠BED=∠C+∠EDC=2∠C,
∴∠EDC=∠C,
∴ED=EC,
∴EC=AD
∴BC=BE+EC=AB+AD;t
(3)如图2,过B作BG⊥AC于G,
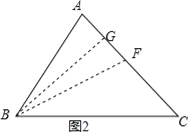
以B为圆心,BA长为半径画弧,交AC于F,
则BF=BA,
在Rt△ABG和Rt△GBG中,
![]() ,
,
∴Rt△ABG≌Rt△GBG,
∴AG=FG,
∴∠BFA=∠A,
∵∠A=2∠C,
∴∠BFA=∠FBC+∠C=2∠C,
∴∠FBC=∠C,
∴FB=FC,
FC=AB,
在Rt△ABG和Rt△BCG中,
BC2=BG2+CG2,
AB2=BG2+AG2
∴BC2﹣AB2=CG2﹣AG2=(CG+AG)(CG﹣AG)
=AC(CG﹣GF)=ACFC
=ACAB.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某完全中学(含初、高中)篮球队12名队员的年龄情况如下:
年龄(单位:岁)
14
15
16
17
18
人 数
1
4
3
2
2
(1)这个队队员年龄的众数是 ,中位数是 ;
(2)求这个队队员的平均年龄;
(3)若把这个队队员年龄绘成扇形统计图,请求出年龄为15岁对应的圆心角的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,∠ABC=45
 ,CD⊥AB于D,BE平分∠ABC,且BE⊥AC于E,与CD相交于点F,H是BC边的中点,连结DH,与BE相交于点G.
,CD⊥AB于D,BE平分∠ABC,且BE⊥AC于E,与CD相交于点F,H是BC边的中点,连结DH,与BE相交于点G.(1)求证:BF=AC;
(2)求证:CE=
 BF.
BF.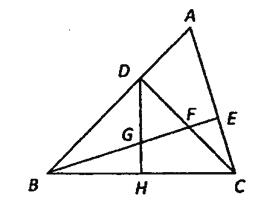
-
科目: 来源: 题型:
查看答案和解析>>【题目】25的平方根是( )
A.±5 B.﹣5 C.5 D.25
-
科目: 来源: 题型:
查看答案和解析>>【题目】用汽车运一批货物,第一次运走总数的45%,第二次运走75吨,还剩下35吨,这批货物共有多少吨?
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个车间加工轴杆和轴承,平均每人每天可以加工轴杆12根或轴承15个.车间共90人,应该怎样分配人,才能使每天生产的轴杆和轴承正好配套(一根轴杆和一个轴承恰好配成一套)?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,如图,△ABC中,∠C=90°,E为BC边中点.
(1)尺规作图:以AC边为直径,作⊙O,交AB于点D(保留作图痕迹,标上相应的字母,可不写作法);
(2)连结DE,求证:DE为⊙O的切线;
(3)若AD=4,BD=
 ,求DE的长.
,求DE的长.
相关试题

