【题目】某完全中学(含初、高中)篮球队12名队员的年龄情况如下:
年龄(单位:岁) | 14 | 15 | 16 | 17 | 18 |
人 数 | 1 | 4 | 3 | 2 | 2 |
(1)这个队队员年龄的众数是 ,中位数是 ;
(2)求这个队队员的平均年龄;
(3)若把这个队队员年龄绘成扇形统计图,请求出年龄为15岁对应的圆心角的度数.
参考答案:
【答案】(1)15,16;(2)16;(3)120°
【解析】试题分析:(1)众数就是出现次数最多的数,而中位数就是大小处于中间位置的数,根据定义即可求解;
(2)利用求平均数公式计算即可;
(3)年龄为15岁所占的百分比,乘以360即可得到结果.
试题解析:1)15岁出现了4次,次数最多,因而众数是:15;
12个数,处于中间位置的都是16,因而中位数是:16.
(2)这个队队员的平均年龄=![]() =16(岁);
=16(岁);
(3)年龄为15岁对应的圆心角的度=![]() ×360°=120°.
×360°=120°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知方程(a﹣2)x2+2ax﹣12=0是关于x的一元一次方程,则a=_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形ABCD中,DE⊥AC于点E,∠EDC:∠EDA=1:3,且AC=12,则DE的长度是______(结果用根号表示).

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点A、B分别位于x轴负、正半轴上,OA、OB﹙OA<OB﹚的长分别是关于x的一元二次方程x2﹣4mx+m2+2=0的两根,C(0,3),且S△ABC=6.
(1)求线段AB的长;
(2)求∠ABC的度数;
(3)过点C作CD⊥AC交x轴于点D,求点D的坐标;
(4)y轴上是否存在点P,使∠PBA=∠ACB?若存在,请求出点P的坐标;若不存在,请说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,∠ABC=45
 ,CD⊥AB于D,BE平分∠ABC,且BE⊥AC于E,与CD相交于点F,H是BC边的中点,连结DH,与BE相交于点G.
,CD⊥AB于D,BE平分∠ABC,且BE⊥AC于E,与CD相交于点F,H是BC边的中点,连结DH,与BE相交于点G.(1)求证:BF=AC;
(2)求证:CE=
 BF.
BF.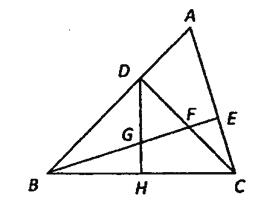
-
科目: 来源: 题型:
查看答案和解析>>【题目】25的平方根是( )
A.±5 B.﹣5 C.5 D.25
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,BD平分∠ABC,∠A=2∠C.
(1)若∠C=38°,则∠ABD= ;
(2)求证:BC=AB+AD;
(3)求证:BC2=AB2+ABAC.

相关试题

