【题目】已知,如图,△ABC中,∠C=90°,E为BC边中点.
(1)尺规作图:以AC边为直径,作⊙O,交AB于点D(保留作图痕迹,标上相应的字母,可不写作法);
(2)连结DE,求证:DE为⊙O的切线;
(3)若AD=4,BD=![]() ,求DE的长.
,求DE的长.

参考答案:
【答案】(1)作图见解析;(2)证明见解析;(3)![]()
【解析】试题分析:(1)作AC的垂直平分线,垂足为O,然后以O点为圆心,OA为半径作圆即可;
(2)如图2,连结OD,CD,根据圆周角定理得到∠ADC=90°,再根据斜边上的中线等于斜边的一半得到DE=EC=BE,则利用等腰三角形的性质得∠1=∠2,加上∠3=∠4,则∠1+∠3=∠2+∠4=90°,于是可根据切线的判定定理可判断DE为⊙O的切线;
(3)证明Rt△BDC∽Rt△BCA,利用相似比计算出BC=![]() ,然后利用斜边上的中线等于斜边的一半即可得到DE的长.
,然后利用斜边上的中线等于斜边的一半即可得到DE的长.
试题解析:(1)解:如图1,

(2)证明:如图2,连结OD,CD,
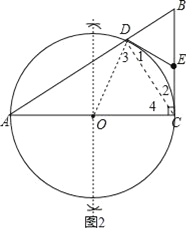
∵AC边为直径,
∴∠ADC=90°,
而E为BC边中点,
∴DE为Rt△BDC斜边BC上的中线,
∴DE=EC=BE,
∴∠1=∠2,
∵OC=OD,
∴∠3=∠4,
∴∠1+∠3=∠2+∠4=∠ACB=90°,
∴OD⊥DE,
∴DE为⊙O的切线;
(3)解:∵∠DBC=∠CBA,
∴Rt△BDC∽Rt△BCA,
∴BC:AB=BD:BC,即BC:(4+![]() )=
)=![]() :BC,
:BC,
∴BC=![]() ,
,
∴DE=![]() BC=
BC=![]()
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,BD平分∠ABC,∠A=2∠C.
(1)若∠C=38°,则∠ABD= ;
(2)求证:BC=AB+AD;
(3)求证:BC2=AB2+ABAC.

-
科目: 来源: 题型:
查看答案和解析>>【题目】用汽车运一批货物,第一次运走总数的45%,第二次运走75吨,还剩下35吨,这批货物共有多少吨?
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个车间加工轴杆和轴承,平均每人每天可以加工轴杆12根或轴承15个.车间共90人,应该怎样分配人,才能使每天生产的轴杆和轴承正好配套(一根轴杆和一个轴承恰好配成一套)?
-
科目: 来源: 题型:
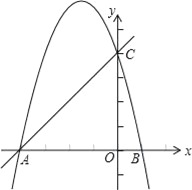
查看答案和解析>>【题目】如图,抛物线y=ax2﹣bx﹣4a交x轴于点A、B,交y轴于点C,其中点B、C的坐标分别为B(1,0)、C(0,4).
(1)求抛物线的解析式,并用配方法把其化为y=a(x﹣h)2+k的形式,写出顶点坐标;
(2)已知点D(m,1﹣m)在第二象限的抛物线上,求出m的值,并直接写出点D关于直线AC的对称点E的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校为美化校园,计划对面积为1800m2的区域进行绿化,安排甲、乙两个工程队完成.已知甲队每天能完成绿化的面积是乙队每天能完成绿化的面积的2倍,并且在独立完成面积为400m2区域的绿化时,甲队比乙队少用4天.
(1)求甲、乙两工程队每天能完成绿化的面积分别是多少m2?
(2)若学校每天需付给甲队的绿化费用为0.4万元,乙队为0.25万元,要使这次的绿化总费用不超过8万元,至少应安排甲队工作多少天?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果一个角的补角是142°,那么这个角的余角是 .
相关试题

