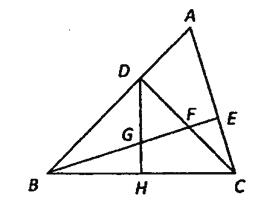
【题目】如图,△ABC中,∠ABC=45![]() ,CD⊥AB于D,BE平分∠ABC,且BE⊥AC于E,与CD相交于点F,H是BC边的中点,连结DH,与BE相交于点G.
,CD⊥AB于D,BE平分∠ABC,且BE⊥AC于E,与CD相交于点F,H是BC边的中点,连结DH,与BE相交于点G.
(1)求证:BF=AC;
(2)求证:CE=![]() BF.
BF.
参考答案:
【答案】(1)证明见解析;(2)证明见解析.
【解析】试题分析:(1)根据三角形的内角和定理求出∠A=∠DFB,推出BD=DC,根据AAS证出△BDF≌△CDA即可;
(2)推出∠AEB=∠CEB,∠ABE=∠CBE,根据ASA证出△AEB≌△CEB,推出AE=CE即可.
(1)证明:∵CD⊥AB,∠ABC=45°,
∴△BCD是等腰直角三角形.
∴BD=CD.
∵∠DBF=90°-∠BFD,∠DCA=90°-∠EFC,且∠BFD=∠EFC,
∴∠DBF=∠DCA.
在Rt△DFB和Rt△DAC中,∠BDF=∠CDA,
∠A=∠DFB,
BD=DC,
∴Rt△DFB≌Rt△DAC(AAS),
∴BF=AC.
(2)证明:在![]() 和
和![]() 中
中
![]() 平分
平分![]() ,
,
![]() .
.
又![]() ,
,
![]() .
.
![]() .
.
又由(1),知![]() ,
,
![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形ABCD中,DE⊥AC于点E,∠EDC:∠EDA=1:3,且AC=12,则DE的长度是______(结果用根号表示).

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点A、B分别位于x轴负、正半轴上,OA、OB﹙OA<OB﹚的长分别是关于x的一元二次方程x2﹣4mx+m2+2=0的两根,C(0,3),且S△ABC=6.
(1)求线段AB的长;
(2)求∠ABC的度数;
(3)过点C作CD⊥AC交x轴于点D,求点D的坐标;
(4)y轴上是否存在点P,使∠PBA=∠ACB?若存在,请求出点P的坐标;若不存在,请说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某完全中学(含初、高中)篮球队12名队员的年龄情况如下:
年龄(单位:岁)
14
15
16
17
18
人 数
1
4
3
2
2
(1)这个队队员年龄的众数是 ,中位数是 ;
(2)求这个队队员的平均年龄;
(3)若把这个队队员年龄绘成扇形统计图,请求出年龄为15岁对应的圆心角的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】25的平方根是( )
A.±5 B.﹣5 C.5 D.25
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,BD平分∠ABC,∠A=2∠C.
(1)若∠C=38°,则∠ABD= ;
(2)求证:BC=AB+AD;
(3)求证:BC2=AB2+ABAC.

-
科目: 来源: 题型:
查看答案和解析>>【题目】用汽车运一批货物,第一次运走总数的45%,第二次运走75吨,还剩下35吨,这批货物共有多少吨?
相关试题

