【题目】如果一元二次方程 ![]()
![]() 满足
满足 ![]() ,那么我们称这个方程为“阿凡达”方程,已知
,那么我们称这个方程为“阿凡达”方程,已知 ![]() 是“阿凡达”方程,且有两个相等的实数根,则下列结论正确的是( )
是“阿凡达”方程,且有两个相等的实数根,则下列结论正确的是( )
A.![]()
B.![]()
C.![]()
D.![]()
参考答案:
【答案】D
【解析】由定义可知 4 a 2 b + c = 0,表示x=-2是 a x 2 + b x + c = 0 的一个解.
a x 2 + b x + c = 0 是“阿凡达”方程,且有两个相等的实数根,
则(1) 4 a 2 b + c = 0,且(2)b2-4ac=0,
由(1)得4a=2b-c,将它代入(2)得b2-(2b-c)c=0
即(b-c)2=0,
则b=c.
故选D.
【考点精析】利用求根公式对题目进行判断即可得到答案,需要熟知根的判别式△=b2-4ac,这里可以分为3种情况:1、当△>0时,一元二次方程有2个不相等的实数根2、当△=0时,一元二次方程有2个相同的实数根3、当△<0时,一元二次方程没有实数根.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,正方形ABCD的边长为2,点M是BC的中点,P是线段MC上的一个动点(不与M、C重合),以AB为直径作⊙O,过点P作⊙O的切线,交AD于点F,切点为E.
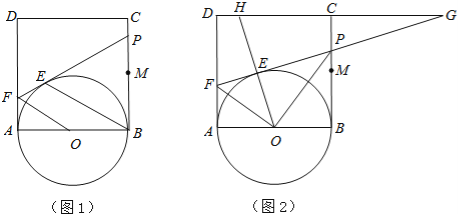
(1)求证:OF∥BE;
(2)设BP=x,AF=y,求y关于x的函数解析式,并写出自变量x的取值范围;
(3)延长DC、FP交于点G,连接OE并延长交直线DC与H(图2),问是否存在点P,使△EFO∽△EHG(E、F、O与E、H、G为对应点)?如果存在,试求(2)中x和y的值;如果不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,C是线段AB的中点,CD平分∠ACE,CE平分∠BCD,CD=CE;

(1)求证:△ACD≌△BCE;
(2)若∠D=50°,求∠B的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(8分)某体育馆计划从一家体育用品商店一次性购买若干个气排球和篮球(每个气排球的价格都相同,每个篮球的价格都相同).经洽谈,购买1个气排球和2个篮球共需210元;购买2个气排球和3个篮球共需340元.
(1)每个气排球和每个篮球的价格各是多少元?
(2)该体育馆决定从这家体育用品商店一次性购买气排球和篮球共50个,总费用不超过3200元,且购买气排球的个数少于30个,应选择哪种购买方案可使总费用最低?最低费用是多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】将方程x2-8x=10化为一元二次方程的一般形式,其中一次项系数、常数项分别是( )
A.-8、-10B.-8、10C.8、-10D.8、10
-
科目: 来源: 题型:
查看答案和解析>>【题目】请选择适当的方法解下列一元二次方程:
(1)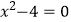
(2)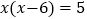
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,E、F是平行四边行ABCD的对角线AC上的 两点,AE=CF。
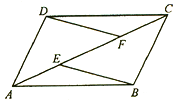
求证:
(1)△ADF≌△CBE
(2)EB∥DF.
相关试题

