【题目】已知:如图,E、F是平行四边行ABCD的对角线AC上的 两点,AE=CF。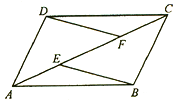
求证:
(1)△ADF≌△CBE
(2)EB∥DF.
参考答案:
【答案】
(1)
证明:∵四边行ABCD是平行四边形,
∴AD=BC,AD∥BC,
∴∠DAF=∠BCE,
∵AE=CF,
∴AF=CE.
在△ADF和△CBE中,
|
∴△ADF≌△CBE(SAS).
;
;
;
;
;
;
(2)
(2)∵△ADF≌△CBE,
∴∠DFA=∠BEC ,
∴DF∥EB
【解析】(1)由平行四边形的性质得到AD=BC,AD∥BC,和AE=CF去证明;
(2)由(1)△ADF≌△CBE,得到∠DFA=∠BEC , 由内错角相等可知DF∥EB.
【考点精析】解答此题的关键在于理解平行线的性质的相关知识,掌握两直线平行,同位角相等;两直线平行,内错角相等;两直线平行,同旁内角互补,以及对平行四边形的性质的理解,了解平行四边形的对边相等且平行;平行四边形的对角相等,邻角互补;平行四边形的对角线互相平分.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果一元二次方程
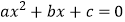
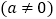 满足
满足 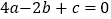 ,那么我们称这个方程为“阿凡达”方程,已知
,那么我们称这个方程为“阿凡达”方程,已知 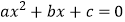 是“阿凡达”方程,且有两个相等的实数根,则下列结论正确的是( )
是“阿凡达”方程,且有两个相等的实数根,则下列结论正确的是( )
A.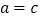
B.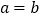
C.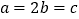
D.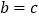
-
科目: 来源: 题型:
查看答案和解析>>【题目】将方程x2-8x=10化为一元二次方程的一般形式,其中一次项系数、常数项分别是( )
A.-8、-10B.-8、10C.8、-10D.8、10
-
科目: 来源: 题型:
查看答案和解析>>【题目】请选择适当的方法解下列一元二次方程:
(1)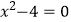
(2)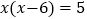
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法正确的是( )
A. 射线AB和射线BA是两条不同的射线 B. 过三点可以画三条直线
C. 两点之间,直线最短 D. -a是负数
-
科目: 来源: 题型:
查看答案和解析>>【题目】观察下列三行数:
﹣2,4,﹣8,16,﹣32,64,…
﹣1,3,﹣7,17,﹣31,65,…
﹣
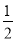 ,1,﹣2,4,﹣8,16…
,1,﹣2,4,﹣8,16…(1)第①行数按什么规律排列?
(2)第②、③与第①行数分别有什么关系?
(3)取每行的第10个数,计算这三个数的和.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一件商品以进价120%的价格标价,后又打八折出售,最后这件商品是( )
A. 赚了 B. 亏了 C. 不赚不亏 D. 不确定盈亏
相关试题

