【题目】我们约定,在平面直角坐标系![]() 中,经过象限内某点且平行于坐标轴或平行于两坐标轴夹角平分线的直线,叫该点的“参照线”.例如,点
中,经过象限内某点且平行于坐标轴或平行于两坐标轴夹角平分线的直线,叫该点的“参照线”.例如,点![]() 的参照线有:
的参照线有:![]() ,
,![]() ,
,![]() ,
,![]() (如图1).
(如图1).
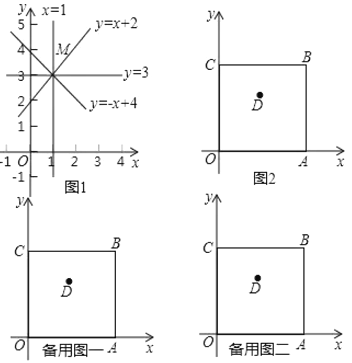
如图2,正方形![]() 在平面直角坐标系
在平面直角坐标系![]() 中,点
中,点![]() 在第一象限,点
在第一象限,点![]() ,
,![]() 分别在
分别在![]() 轴和
轴和![]() 轴上,点
轴上,点![]() 在正方形内部.
在正方形内部.
(1)直接写出点![]() 的所有参照线: ;
的所有参照线: ;
(2)若![]() ,点
,点![]() 在线段
在线段![]() 的垂直平分线上,且点
的垂直平分线上,且点![]() 有一条参照线是
有一条参照线是![]() ,则点
,则点![]() 的坐标是_______________;
的坐标是_______________;
(3)在(2)的条件下,点![]() 是
是![]() 边上任意一点(点
边上任意一点(点![]() 不与点
不与点![]() ,
,![]() 重合),连接
重合),连接![]() ,将
,将![]() 沿着
沿着![]() 折叠,点
折叠,点![]() 的对应点记为
的对应点记为![]() .当点
.当点![]() 在点
在点![]() 的平行于坐标轴的参照线上时,写出相应的折痕
的平行于坐标轴的参照线上时,写出相应的折痕![]() 所在直线的解析式: .
所在直线的解析式: .
参考答案:
【答案】(1)x=m,y=n,y=x+n-m,y=-x+n+m;(2)(3,4);(3)![]() 或
或![]() .
.
【解析】
(1)根据参照线的定义可知,点D(m,n)的所有参照线为:x=m,y=n,y=x+n-m,y=-x+n+m;
(2)利用待定系数法即可解决问题;
(3)分两种情形①如图1中,当点A′在参照线HM上时,设PA=PA′=x.②如图2中,当点A′在参照线DH上时,设PA=PA′=y.分别构建方程即可解决问题;
解:(1)根据参照线的定义可知,点D(m,n)的所有参照线为:x=m,y=n,y=x+n-m,y=-x+n+m,
故答案为x=m,y=n,y=x+n-m,y=-x+n+m
(2)∵A(6,0),点D在线段OA的垂直平分线上,
∴点D的横坐标为3,
又∵点D有一条参照线是y=-x+7,
∴x=3时,y=-3+7=4,
∴点D坐标为(3,4),
故答案为(3,4).
(3)①如图1中,当点A′在参照线HM上时,设PA=PA′=x.

易知 ![]()
![]()
![]()
在![]() 中,
中,![]()
![]()
![]()
![]()
∴直线OP的解析式为:
![]()
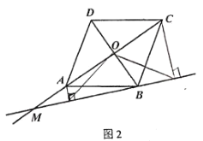
②如图2中,当点A′在参照线DH上时,设PA=PA′=y.
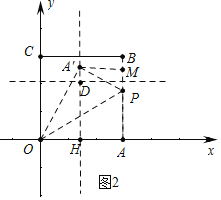
易知 ![]()
在![]() 中,
中,![]()
![]()
![]()
![]()
∴直线OP的解析式为:
![]()
故答案为: ![]() 或
或![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形ABCD中,对角线AC、BD相交于点G,E、F分别是边AD、BC的中点,AB=2,BC=4,一动点P从点B出发,沿着B﹣A﹣D﹣C的方向在矩形的边上运动,运动到点C停止.点M为图1中的某个定点,设点P运动的路程为x,△BPM的面积为y,表示y与x的函数关系的图象大致如图2所示.那么,点M的位置可能是图1中的( )

A. 点CB. 点EC. 点FD. 点G
-
科目: 来源: 题型:
查看答案和解析>>【题目】《九章算术》是中国传统数学最重要的著作,奠定了中国传统数学的基本框架,书中的算法体系至今仍在推动着计算机的发展和应用.《九章算术》中记载:今有户不知高、广,竿不知长、短.横之不出四尺,从之不出二尺,邪之适出.问户高、广、邪各几何?译文是:今有门不知其高、宽,有竿,不知其长、短,横放,竿比门宽长出
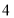 尺;竖放,竿比门高长出
尺;竖放,竿比门高长出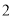 尺;斜放,竿与门对角线恰好相等.问门高、宽、对角线长分别是多少?若设门对角线长为
尺;斜放,竿与门对角线恰好相等.问门高、宽、对角线长分别是多少?若设门对角线长为 尺,则可列方程为__________.
尺,则可列方程为__________. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形OABC的两边OA、OC分别在x轴、y轴上,点D(5,3)在边AB上,以C为中心,把△CDB旋转90°,则旋转后点D的对应点D′的坐标是 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图是二次函数y=ax2+bx+c图象的一部分,图象过点A(-3,0),对称轴为直线x=-1,给出四个结论:①b2>4ac;②2a+b=0;③a+b+c>0;④若点B(-
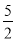 ,y1),C(-
,y1),C(-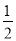 ,y2)为函数图象上的两点,则y1<y2.其中正确结论是___________.
,y2)为函数图象上的两点,则y1<y2.其中正确结论是___________.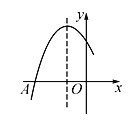
-
科目: 来源: 题型:
查看答案和解析>>【题目】同学们,在初一学习正多边形和圆这节课时,我们就学习过四边形的内角和等于360°.下面我们就在四边形中来研究几个问题:
(1)问题背景:
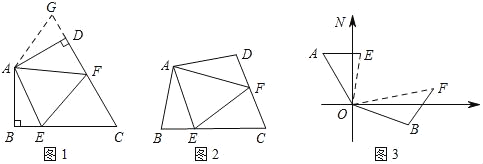
如图1:在四边形ABCD中,AB=AD,∠BAD=120°,∠B=∠ADC=90°,E、F分别是BC、CD上的点,且∠EAF=60°,探究图中线段BE、EF、FD之间的数量关系.
小王同学探究此问题的方法是,延长FD到点G,使DG=BE.连结AG,先证明△ABE≌△ADG,再证明△AEF≌△AGF,可得出结论,他的结论应是______;
(2)探索延伸:
如图2,若在四边形ABCD中,AB=AD,∠B+∠D=180°,E、F分别是BC、CD上的点,且∠EAF=
 ∠BAD,上述结论是否仍成立,并说明理由;
∠BAD,上述结论是否仍成立,并说明理由;(3)实际应用:
如图3,在某次军事演习中,舰艇甲在指挥中心(点O处)北偏西30°的A处,舰艇乙在指挥中心南偏东70°的B处,并且两舰艇到指挥中心的距离相等.接到行动指令后,舰艇甲向正东方向以45海里/时的速度前进,同时,舰艇乙沿北偏西50°的方向以60海里/时的速度前进,2小时后,指挥中心观察到甲、乙两舰艇分别到达E、F处,且两舰艇之间的夹角为70°,试求此时两舰艇之间的距离.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
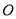 为菱形
为菱形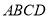 对角线的交点,
对角线的交点, 是射线
是射线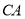 上的一个动点(点
上的一个动点(点 与点
与点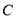 ,
,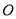 ,
,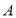 都不重合),过点
都不重合),过点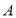 ,
,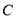 分别向直线
分别向直线 作垂线段,垂足分别为
作垂线段,垂足分别为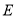 ,
,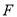 ,连接
,连接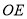 ,
,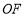 .
.(1)①当点
 在线段
在线段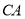 上时,在图1中依据题意补全图形:
上时,在图1中依据题意补全图形:②猜想
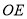 与
与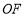 的数量关系为 .
的数量关系为 .(2)小东通过观察、实验发现点
 在线段
在线段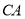 的延长线上运动时,(1)中的猜想始终成立.
的延长线上运动时,(1)中的猜想始终成立.小东把这个发现与同学们进行交流,通过讨论,形成了证明此猜想的几种想法:
想法1:由已知条件和菱形对角线互相平分,可以构造与
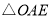 全等的三角形,从而得到相等的钱段,再依据直角三角形斜边中线的性质,即可证明猜想;
全等的三角形,从而得到相等的钱段,再依据直角三角形斜边中线的性质,即可证明猜想;想法2:由已知条件和菱形对角线互相垂直,能找到两组共斜边的直角三角形,例如其中的一组
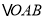 和
和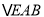 ,再依据直角三角形斜边中线的性质,菱形四条边相等,可以构造一对以
,再依据直角三角形斜边中线的性质,菱形四条边相等,可以构造一对以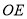 和
和 为对应边的全等三角形,即可证明猜想.
为对应边的全等三角形,即可证明猜想.…
请你参考上面的想法,在图2中帮助小东完成画图,并证明此猜想(一种方法即可).
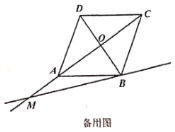
(3)当
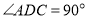 时,请直接写出线段
时,请直接写出线段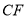 ,
,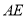 ,
,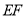 之间的数量关系是 .
之间的数量关系是 .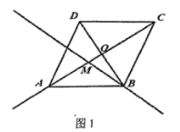
相关试题

