【题目】如图,已知直线y=ax+b与双曲线y= ![]() (x>0)交于A(x1 , y1),B(x2 , y2)两点(A与B不重合),直线AB与x轴交于P(x0 , 0),与y轴交于点C.
(x>0)交于A(x1 , y1),B(x2 , y2)两点(A与B不重合),直线AB与x轴交于P(x0 , 0),与y轴交于点C. 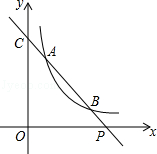
(1)若A,B两点坐标分别为(1,3),(3,y2),求点P的坐标.
(2)若b=y1+1,点P的坐标为(6,0),且AB=BP,求A,B两点的坐标.
(3)结合(1),(2)中的结果,猜想并用等式表示x1 , x2 , x0之间的关系(不要求证明).
参考答案:
【答案】
(1)解:∵直线y=ax+b与双曲线y= ![]() (x>0)交于A(1,3),
(x>0)交于A(1,3),
∴k=1×3=3,
∴y= ![]() ,
,
∵B(3,y2)在反比例函数的图象上,
∴y2= ![]() =1,
=1,
∴B(3,1),
∵直线y=ax+b经过A、B两点,
∴ ![]() 解得
解得 ![]() ,
,
∴直线为y=﹣x+4,
令y=0,则x=4,
∴P(4,O)
(2)解:如图,作AD⊥y轴于D,AE⊥x轴于E,BF⊥x轴于F,BG⊥y轴于G,AE、BG交于H,
则AD∥BG∥x轴,AE∥BF∥y轴,
∴ ![]() =
= ![]() ,
, ![]() =
= ![]() =
= ![]() ,
,
∵b=y1+1,AB=BP,
∴ ![]() =
= ![]() ,
,
![]() =
= ![]() =
= ![]() ,
,
∴B( ![]() ,
, ![]() y1)
y1)
∵A,B两点都是反比例函数图象上的点,
∴x1y1= ![]()
![]() y1,
y1,
解得x1=2,
代入 ![]() =
= ![]() ,解得y1=2,
,解得y1=2,
∴A(2,2),B(4,1)
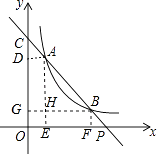
(3)解:根据(1),(2)中的结果,猜想:x1,x2,x0之间的关系为x1+x2=x0
【解析】(1)先把A(1,3)),B(3,y2)代入y= ![]() 求得反比例函数的解析式,进而求得B的坐标,然后把A、B代入y=x+b利用待定系数法即可求得直线的解析式,继而即可求得P的坐标;(2)作AD⊥y轴于D,AE⊥x轴于E,BF⊥x轴于F,BG⊥y轴于G,AE、BG交于H,则AD∥BG∥x轴,AE∥BF∥y轴,得出
求得反比例函数的解析式,进而求得B的坐标,然后把A、B代入y=x+b利用待定系数法即可求得直线的解析式,继而即可求得P的坐标;(2)作AD⊥y轴于D,AE⊥x轴于E,BF⊥x轴于F,BG⊥y轴于G,AE、BG交于H,则AD∥BG∥x轴,AE∥BF∥y轴,得出 ![]() =
= ![]() ,
, ![]() =
= ![]() =
= ![]() ,根据题意得出
,根据题意得出 ![]() =
= ![]() ,
, ![]() =
= ![]() =
= ![]() ,从而求得B(
,从而求得B( ![]() ,
, ![]() y1),然后根据k=xy得出x1y1=
y1),然后根据k=xy得出x1y1= ![]()
![]() y1 , 求得x1=2,代入
y1 , 求得x1=2,代入 ![]() =
= ![]() ,解得y1=2,即可求得A、B的坐标;(3)合(1),(2)中的结果,猜想x1+x2=x0 .
,解得y1=2,即可求得A、B的坐标;(3)合(1),(2)中的结果,猜想x1+x2=x0 .
-
科目: 来源: 题型:
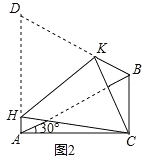
查看答案和解析>>【题目】如图1,在△ABC中,∠ACB=90°,∠CAB=30°,△ABD是等边三角形,E是AB的中点,连接CE并延长交AD于F.
(1)求证:△AEF≌△BEC;
(2)判断四边形BCFD是何特殊四边形,并说出理由;
(3)如图2,将四边形ACBD折叠,使D与C重合,HK为折痕,若BC=1,求AH的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某体育馆计划从一家体育用品商店一次性购买若干个气排球和篮球(每个气排球的价格都相同,每个篮球的价格都相同).经洽谈,购买1个气排球和2个篮球共需210元;购买2个气排球和3个篮球共需340元.
(1)每个气排球和每个篮球的价格各是多少元?
(2)该体育馆决定从这家体育用品商店一次性购买气排球和篮球共50个,总费用不超过3200元,且购买气排球的个数少于30个,应选择哪种购买方案可使总费用最低?最低费用是多少元? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,某校少年宫数学课外活动初三小组的同学为测量一座铁塔AM的高度如图,他们在坡度是i=1:2.5的斜坡DE的D处,测得楼顶的移动通讯基站铁塔的顶部A和楼顶B的仰角分别是60°、45°,斜坡高EF=2米,CE=13米,CH=2米.大家根据所学知识很快计算出了铁塔高AM.亲爱的同学们,相信你也能计算出铁塔AM的高度!请你写出解答过程.(数据
 ≈1.41,
≈1.41, 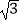 ≈1.73供选用,结果保留整数)
≈1.73供选用,结果保留整数)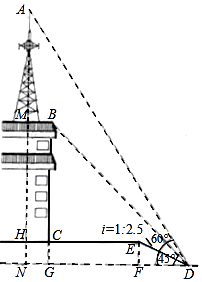
-
科目: 来源: 题型:
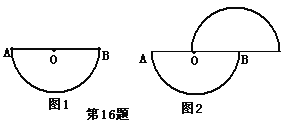
查看答案和解析>>【题目】以图1(以O为圆心,半径1 的半圆)作为“基本图形”,分别经历如下变换能得到图2的序号是 (多填或错填得0分,少填酌情给分)
①只要向右平移1个 单位;
② 先以直线AB为对称轴进行对称变换,再向右平移1个单位;
③先绕着O旋转180°,再向右平移1个单位;
④只要绕着某点旋转180°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB是⊙O的直径,点C为⊙O上一点,AE和过点C的切线互相垂直,垂足为E,AE交⊙O于点D,直线EC交AB的延长线于点P,连接AC,BC,PB:PC=1:2.

(1)求证:AC平分∠BAD;
(2)探究线段PB,AB之间的数量关系,并说明理由;
(3)若AD=3,求△ABC的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,正方形ABCD的边长为2,点M是BC的中点,P是线段MC上的一个动点(不与M、C重合),以AB为直径作⊙O,过点P作⊙O的切线,交AD于点F,切点为E.

(1)求证:OF∥BE;
(2)设BP=x,AF=y,求y关于x的函数解析式,并写出自变量x的取值范围;
(3)延长DC、FP交于点G,连接OE并延长交直线DC于H(图2),问是否存在点P,使△EFO∽△EHG(E、F、O与E、H、G为对应点)?如果存在,试求(2)中x和y的值;如果不存在,请说明理由.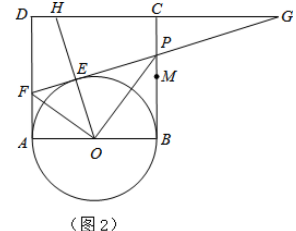
相关试题

