【题目】如图1,在△ABC中,∠ACB=90°,∠CAB=30°,△ABD是等边三角形,E是AB的中点,连接CE并延长交AD于F.
(1)求证:△AEF≌△BEC;
(2)判断四边形BCFD是何特殊四边形,并说出理由;
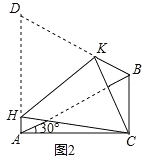
(3)如图2,将四边形ACBD折叠,使D与C重合,HK为折痕,若BC=1,求AH的长.

参考答案:
【答案】(1)(2)见解析;(3)![]()
【解析】试题分析:(1)在△ABC中,由已知可得∠ABC=60°,从而推得∠BAD=∠ABC=60°.由E为AB的中点,得到AE=BE.又因为∠AEF=∠BEC,所以△AEF≌△BEC;(2)在Rt△ABC中,E为AB的中点,则CE=![]() AB,BE=
AB,BE=![]() AB,得到∠BCE=∠EBC=60°.由△AEF≌△BEC,得∠AFE=∠BCE=60°.又∠D=60°,得∠AFE=∠D=60度.所以FC∥BD,又因为∠BAD=∠ABC=60°,所以AD∥BC,即FD∥BC,则四边形BCFD是平行四边形.
AB,得到∠BCE=∠EBC=60°.由△AEF≌△BEC,得∠AFE=∠BCE=60°.又∠D=60°,得∠AFE=∠D=60度.所以FC∥BD,又因为∠BAD=∠ABC=60°,所以AD∥BC,即FD∥BC,则四边形BCFD是平行四边形.
(2)由∠BAD=60°,∠CAB=30°,可得∠CAH=90°;在Rt△ABC中,∠CAB=30°,BC=1,根据30°角的直角三角形的性质可得AB=2BC=2,所以AD=AB=2.设AH=x,则HC=HD=AD﹣AH=2﹣x,在Rt△ABC中,由勾股定理求得AC2=3,在Rt△ACH中,根据勾股定理列出方程x2+3=(2﹣x)2,解方程即可求得AH的值.
试题解析:
(1)证明:①在△ABC中,∠ACB=90°,∠CAB=30°,∴∠ABC=60°.
在等边△ABD中,∠BAD=60°,∴∠BAD=∠ABC=60°.
∵E为AB的中点,∴AE=BE.又∵∠AEF=∠BEC,∴△AEF≌△BEC.
(2)在△ABC中,∠ACB=90°,E为AB的中点,
∴CE=![]() AB,BE=
AB,BE=![]() AB.∴CE=AE,∴∠EAC=∠ECA=30°,∴∠BCE=∠EBC=60°.
AB.∴CE=AE,∴∠EAC=∠ECA=30°,∴∠BCE=∠EBC=60°.
又∵△AEF≌△BEC,∴∠AFE=∠BCE=60°.
又∵∠D=60°,∴∠AFE=∠D=60°.∴FC∥BD.
又∵∠BAD=∠ABC=60°,∴AD∥BC,即FD∥BC.∴四边形BCFD是平行四边形
(3)∵∠BAD=60°,∠CAB=30°,∴∠CAH=90°.
在Rt△ABC中,∠CAB=30°,BC=1,∴AB=2BC=2.∴AD=AB=2.
设AH=x,则HC=HD=AD﹣AH=2﹣x,在Rt△ABC中,AC2=22﹣12=3,
在Rt△ACH中,AH2+AC2=HC2,即x2+3=(2﹣x)2,解得x=![]() ,即AH=
,即AH=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读以下内容,并解决所提出的问题:
 我们知道:
我们知道: ;
;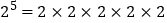 ;所以
;所以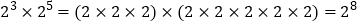 .
. 用与
用与 相同的方法可计算得
相同的方法可计算得 ;
;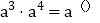 .
. 归纳以上的学习过程,可猜测结论:
归纳以上的学习过程,可猜测结论: ________.
________. 利用以上的结论计算以下各题:①
利用以上的结论计算以下各题:① ________;②
________;② =________.
=________. -
科目: 来源: 题型:
查看答案和解析>>【题目】“佳佳商场”在销售某种进货价为20元/件的商品时,以30元/件售出,每天能售出100件.调查表明:这种商品的售价每上涨1元/件,其销售量就将减少2件.
(1)为了实现每天1600元的销售利润,“佳佳商场”应将这种商品的售价定为多少?
(2)物价局规定该商品的售价不能超过40元/件,“佳佳商场”为了获得最大的利润,应将该商品售价定为多少?最大利润是多少? -
科目: 来源: 题型:
查看答案和解析>>【题目】现代互联网技术的广泛应用,催生了快递行业的告诉发展,小明计划给朋友快递一部分物品,经了解有甲乙两家快递公司比较合适.甲公司表示:快递物品不超过
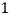 千克的,按每千克
千克的,按每千克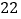 元收费;超过
元收费;超过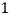 千克,超过的部分按每千克
千克,超过的部分按每千克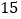 元收费.设小明快递物品
元收费.设小明快递物品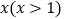 千克.
千克.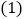 用含有
用含有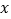 的代数式表示小明快递物品的费用;
的代数式表示小明快递物品的费用;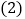 若小明快递物品
若小明快递物品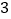 千克,应付快递费多少元?
千克,应付快递费多少元? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将矩形ABCD沿对角线AC折叠,使B落在E处,AE交CD于点F,则下列结论中不一定成立的是( )

A.AD=CE
B.AF=CF
C.△ADF≌△CEF
D.∠DAF=∠CAF -
科目: 来源: 题型:
查看答案和解析>>【题目】某厂一周计划每天生产400辆自行车,实际生产量(单位:辆)分别为405,393,410,409,387,406,397.
(1)用正、负数表示实际生产量与计划量的增减情况;
(2)该厂实际共生产多少辆自行车?平均每天生产多少辆自行车
-
科目: 来源: 题型:
查看答案和解析>>【题目】函数 y=
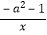 (a为常数)的图象上有三点(﹣4,y1),(﹣1,y2),(2,y3),则函数值y1 , y2 , y3的大小关系是( )
(a为常数)的图象上有三点(﹣4,y1),(﹣1,y2),(2,y3),则函数值y1 , y2 , y3的大小关系是( )
A.y3<y1<y2
B.y3<y2<y1
C.y1<y2<y3
D.y2<y3<y1
相关试题

