【题目】在△ABC中,BC=AC,∠BCA=90°,P为直线AC上一点,过点A作AD⊥BP于点D,交直线BC于点Q.
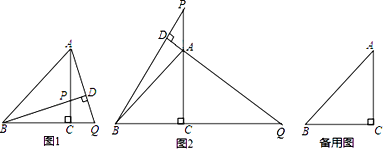
(1)如图1,当P在线段AC上时,求证:BP=AQ;
(2)如图2,当P在线段CA的延长线上时,(1)中的结论是否成立?________(填“成立”或“不成立”)
(3)在(2)的条件下,当∠DBA=________时,存在AQ=2BD,说明理由.
参考答案:
【答案】(1)详见解析;(2)成立; (3)22.5°,理由详见解析.
【解析】试题分析:(1)首先根据内角和定理得出∠DAP=∠CBP,进而得出
△ACQ≌△BCP即可得出答案;
(2)延长BA交PQ于H,由于![]() 得到
得到![]() 推出△AQC≌△BPC(ASA),即可得出结论;
推出△AQC≌△BPC(ASA),即可得出结论;
(3)当![]() 时,存在
时,存在![]() 根据等腰三角形的性质得到BP=2BD,通过△PBC≌△ACQ,根据全等三角形的性质即可得到结论.
根据等腰三角形的性质得到BP=2BD,通过△PBC≌△ACQ,根据全等三角形的性质即可得到结论.
试题解析:
(1)证明:∵∠ACB=∠ADB=90°,∠APD=∠BPC,
∴∠DAP=∠CBP,
在△ACQ和△BCP中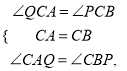
∴△ACQ≌△BCP(ASA),
∴BP=AQ
(2)成立,
理由:延长BA交PQ于H,
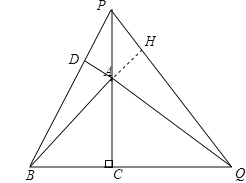
![]() ∠AQC=∠BQD,
∠AQC=∠BQD,
∴∠CAQ=∠DBQ,
在△AQC和△BPC中,
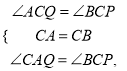
∴△AQC≌△BPC(ASA),
∴AQ=BP,
故答案为:成立;
(3)22.5°,
当∠DBA=22.5°时,存在AQ=2BD,
理由:∵∠BAC=∠DBA+∠APB=45°,
∴∠PBA=∠APB=22.5°,
∴AP=AB,
∵AD⊥BP,
∴BP=2BD,
在△PBC与△QAC中,
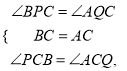
∴△PBC≌△ACQ,
∴AQ=PB,
∴AQ=2BD.
故答案为:22.5°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列命题是真命题的是( )
A.邻补角相等
B.同位角相等
C.两直线平行,同旁内角相等
D.对顶角相等
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,对面积为s的△ABC逐次进行以下操作:
第一次操作,分别延长AB、BC、CA至点A1、B1、C1,使得A1B=2AB,B1C=2BC,C1A=2CA,顺次连接A1、B1、C1,得到△A1B1C1,记其面积为S1;
第二次操作,分别延长A1B1、B1C1、C1A1至点A2、B2、C2,使得A2B1=2A1B1,B2C1=2B1C1,C2A1=2C1A1顺次连接A2、B2、C2,得到△A2B2C2,记其面积为S2;
…;
按此规律继续下去,可得到△AnBnCn,则其面积Sn=______.

-
科目: 来源: 题型:
查看答案和解析>>【题目】二次函数y=ax2+bx的图像如图,若一元二次方程ax2+bx+m=0有实数根,则m的最大值为( )

A.﹣3
B.3
C.﹣6
D.9 -
科目: 来源: 题型:
查看答案和解析>>【题目】在
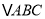 中,
中, 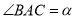 .边
.边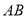 的垂直平分线交边
的垂直平分线交边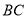 于点
于点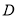 ,边
,边 的垂线交边
的垂线交边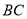 于点
于点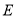 ,连接
,连接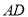 ,
, 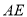 ,则
,则 的度数为__________.(用含
的度数为__________.(用含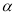 的代数式表示)
的代数式表示) -
科目: 来源: 题型:
查看答案和解析>>【题目】100比80大( ).
A.20%B.25%C.80%D.60%
-
科目: 来源: 题型:
查看答案和解析>>【题目】在一个长8 厘米,宽6厘米的长方形中,剪下一个最大的圆,这个圆的面积是( )平方厘米.
A.18.84B.28.26C.25.12D.50.24
相关试题

