【题目】二次函数y=ax2+bx的图像如图,若一元二次方程ax2+bx+m=0有实数根,则m的最大值为( ) 
A.﹣3
B.3
C.﹣6
D.9
参考答案:
【答案】B
【解析】解:(法1)∵抛物线的开口向上,顶点纵坐标为﹣3, ∴a>0, ![]() =﹣3,即b2=12a,
=﹣3,即b2=12a,
∵一元二次方程ax2+bx+m=0有实数根,
∴△=b2﹣4am≥0,即12a﹣4am≥0,即12﹣4m≥0,解得m≤3,
∴m的最大值为3.
(法2)一元二次方程ax2+bx+m=0有实数根,
可以理解为y=ax2+bx和y=﹣m有交点,
可见﹣m≥﹣3,
∴m≤3,
∴m的最大值为3.
故选B.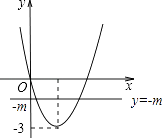
【考点精析】关于本题考查的抛物线与坐标轴的交点,需要了解一元二次方程的解是其对应的二次函数的图像与x轴的交点坐标.因此一元二次方程中的b2-4ac,在二次函数中表示图像与x轴是否有交点.当b2-4ac>0时,图像与x轴有两个交点;当b2-4ac=0时,图像与x轴有一个交点;当b2-4ac<0时,图像与x轴没有交点.才能得出正确答案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,∠ABC=∠ACB,AD、BD、CD分别平分△ABC的外角∠EAC、内角∠ABC、外角∠ACF.以下结论:
①AD∥BC;
②∠ACB=2∠ADB;
③∠ADC=90°﹣∠ABD;
④BD平分∠ADC;
⑤∠BDC=
 ∠BAC.
∠BAC.其中正确的结论有( )

A.2个 B.3个 C.4个 D.5个
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列命题是真命题的是( )
A.邻补角相等
B.同位角相等
C.两直线平行,同旁内角相等
D.对顶角相等
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,对面积为s的△ABC逐次进行以下操作:
第一次操作,分别延长AB、BC、CA至点A1、B1、C1,使得A1B=2AB,B1C=2BC,C1A=2CA,顺次连接A1、B1、C1,得到△A1B1C1,记其面积为S1;
第二次操作,分别延长A1B1、B1C1、C1A1至点A2、B2、C2,使得A2B1=2A1B1,B2C1=2B1C1,C2A1=2C1A1顺次连接A2、B2、C2,得到△A2B2C2,记其面积为S2;
…;
按此规律继续下去,可得到△AnBnCn,则其面积Sn=______.

-
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,BC=AC,∠BCA=90°,P为直线AC上一点,过点A作AD⊥BP于点D,交直线BC于点Q.
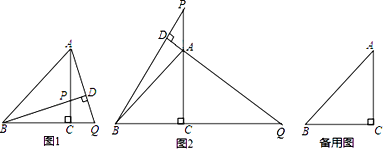
(1)如图1,当P在线段AC上时,求证:BP=AQ;
(2)如图2,当P在线段CA的延长线上时,(1)中的结论是否成立?________(填“成立”或“不成立”)
(3)在(2)的条件下,当∠DBA=________时,存在AQ=2BD,说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在
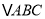 中,
中, 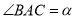 .边
.边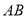 的垂直平分线交边
的垂直平分线交边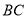 于点
于点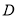 ,边
,边 的垂线交边
的垂线交边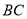 于点
于点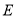 ,连接
,连接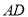 ,
, 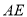 ,则
,则 的度数为__________.(用含
的度数为__________.(用含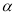 的代数式表示)
的代数式表示) -
科目: 来源: 题型:
查看答案和解析>>【题目】100比80大( ).
A.20%B.25%C.80%D.60%
相关试题

