【题目】小明利用课余时间回收废品,将卖得的钱去购买5本大小不同的两种笔记本,要求共花钱不超过28元,且购买的笔记本的总页数不低于340页,两种笔记本的价格和页数如下表.为了节约资金,小明应选择哪一种购买方案?请说明理由.
大笔记本 | 小笔记本 | |
价格(元/本) | 6 | 5 |
页数(页/本) | 100 | 60 |
参考答案:
【答案】购买1本大笔记本和4本小笔记本;理由见详解.
【解析】
设买大笔记x本,根据共花钱不超过28元,且购买的笔记本的总页数不低于340页,列不等式组;解不等式组,根据x取正整数即可得到满足题意的x值,进而可得不同的方案,再结合表格中的单价进行计算,得到不同方案所对应的花费,然后比较即可求出节约资金的一种方案.
解:设小明购买大笔记本x本,则购买小笔记本(5-x)本.
根据题意,得![]()
解不等式组,得1≤x≤3,故整数解有1,2,3,
∴小明的购买方案共有三种:
第一种:大笔本1本,小笔记本4本,需花费资金1×6+4×5=26(元);
第二种:大笔记本2本,小笔记本3本,需花费资金2×6+3×5=27(元);
第三种:大笔记本3本,小笔记本2本,需花费资金3×6+2×5=28(元).
∵26<27<28,
∴小明应选择第一种购买方案,即购买1本大笔记本和4本小笔记本.
故答案为:购买1本大笔记本和4本小笔记本;理由见详解.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知直线y1=kx+1(k<0)与直线y2=mx(m>0)的交点坐标为(
 ,
, m),则不等式组mx﹣2<kx+1<mx的解集为( )
m),则不等式组mx﹣2<kx+1<mx的解集为( )A. x>
 B.
B.  <x<
<x< C. x<
C. x< D. 0<x<
D. 0<x<
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校为了解学生的每周平均课外阅读时间,在本校随机抽取若干名学生进行调查,并将调查结果绘制成如下不完整的统计图表,请根据图表中所给的信息,解答下列问题:
组别
阅读时间t(单位:小时)
频数(人数)
A
0≤t<1
8
B
1≤t<2
20
C
2≤t<3
24
D
3≤t<4
m
E
4≤t<5
8
F
t≥5
4
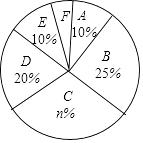
(1)图表中的m= , n=;
(2)扇形统计图中F组所对应的圆心角为度;
(3)该校共有学生1500名,请估计该校有多少名学生的每周平均课外阅读时间不低于3小时? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,根据图中信息解答下列问题:
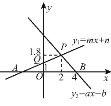
(1)关于x的不等式ax+b>0的解集是 .
(2)关于x的不等式mx+n<1的解集是 .
(3)当x为何值时,y1≤y2?
(4)当x为何值时,0<y2<y1?
-
科目: 来源: 题型:
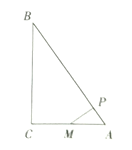
查看答案和解析>>【题目】如图,在△ABC中,∠C=90°,AM=CM,MP⊥AB于点P.求证:BP2=AP2+BC2.
-
科目: 来源: 题型:
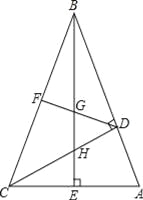
查看答案和解析>>【题目】如图,在△ABC中,∠ABC=45°,CD⊥AB,BE⊥AC,垂足分别为D,E,F为BC中点,BE与DF,DC分别交于点G,H,∠ABE=∠CBE.
(1)线段BH与AC相等吗?若相等给予证明,若不相等请说明理由;
(2)求证:BG2﹣GE2=EA2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在网格中,每个小正方形的边长均为1个单位长度,我们将小正方形的顶点叫做格点,线段AB的端点均在格点上.
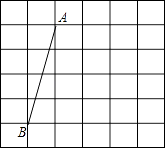
(1)将线段AB向右平移3个单位长度,得到线段A′B′,画出平移后的线段并连接AB′和A′B,两线段相交于点O;
(2)求证:△AOB≌△B′OA′.
相关试题

