【题目】如图,根据图中信息解答下列问题:
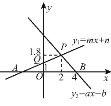
(1)关于x的不等式ax+b>0的解集是 .
(2)关于x的不等式mx+n<1的解集是 .
(3)当x为何值时,y1≤y2?
(4)当x为何值时,0<y2<y1?
参考答案:
【答案】:(1) x<4;(2) x<0;(3)x≤2;(4)2<x<4.
【解析】
(1)求ax+b>0的解集,只需确定直线y2在x轴上方时x的取值范围即可;
(2)求mx+n<1的解集,也就是求直线y1在y=1下方时x的取值范围,据此解答即可;
(3)找出直线y1在直线y2的下方与相交时x的取值范围,据此可确定y1≤y2时x的取值范围;
(4)根据函数图象,找出直线y2在直线y1的下方且在x轴上方时x的取值范围即可.
(1)∵直线y2=ax+b与x轴的交点是(4,0),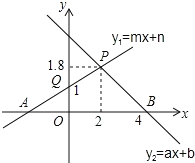
∴当x<4时, y2>0,即不等式ax+b>0的解集是x<4;
(2)∵直线y1=mx+n与y轴的交点是(0,1),
∴当x<0时, y1<1,即不等式mx+n<1的解集是x<0;。
(3)由一次函数的图象知,两条直线的交点坐标是(2,1.8),当函数y1的图象在y2的下面时,有x2,
所以当x2时, y1 y2;
(4)如图所示,当2<x<4时,0< y2< y1.
故答案为:(1) x<4; (2) x<0; (3)x≤2; (4)2<x<4.
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读并完成下列证明:如图,AB∥CD,∠B=55°,∠D=125°,求证:BC∥DE.
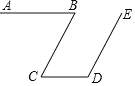
证明:AB∥CD(已知),
∴∠C=∠B( ),又∵∠B=55°( ),
∴∠C=______°(等量代换),
∵∠D=125°( ),
∴
∴BC∥DE( ).
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知直线y1=kx+1(k<0)与直线y2=mx(m>0)的交点坐标为(
 ,
, m),则不等式组mx﹣2<kx+1<mx的解集为( )
m),则不等式组mx﹣2<kx+1<mx的解集为( )A. x>
 B.
B.  <x<
<x< C. x<
C. x< D. 0<x<
D. 0<x<
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校为了解学生的每周平均课外阅读时间,在本校随机抽取若干名学生进行调查,并将调查结果绘制成如下不完整的统计图表,请根据图表中所给的信息,解答下列问题:
组别
阅读时间t(单位:小时)
频数(人数)
A
0≤t<1
8
B
1≤t<2
20
C
2≤t<3
24
D
3≤t<4
m
E
4≤t<5
8
F
t≥5
4
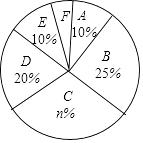
(1)图表中的m= , n=;
(2)扇形统计图中F组所对应的圆心角为度;
(3)该校共有学生1500名,请估计该校有多少名学生的每周平均课外阅读时间不低于3小时? -
科目: 来源: 题型:
查看答案和解析>>【题目】小明利用课余时间回收废品,将卖得的钱去购买5本大小不同的两种笔记本,要求共花钱不超过28元,且购买的笔记本的总页数不低于340页,两种笔记本的价格和页数如下表.为了节约资金,小明应选择哪一种购买方案?请说明理由.
大笔记本
小笔记本
价格(元/本)
6
5
页数(页/本)
100
60
-
科目: 来源: 题型:
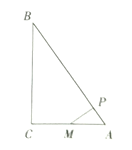
查看答案和解析>>【题目】如图,在△ABC中,∠C=90°,AM=CM,MP⊥AB于点P.求证:BP2=AP2+BC2.
-
科目: 来源: 题型:
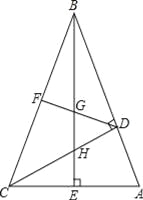
查看答案和解析>>【题目】如图,在△ABC中,∠ABC=45°,CD⊥AB,BE⊥AC,垂足分别为D,E,F为BC中点,BE与DF,DC分别交于点G,H,∠ABE=∠CBE.
(1)线段BH与AC相等吗?若相等给予证明,若不相等请说明理由;
(2)求证:BG2﹣GE2=EA2.
相关试题

