搜索
【题目】两条直线被第三条直线所截，就第三条直线上的两个交点而言形成了“三线八角”
为了便于记忆，同学们可仿照图用双手表示“三线八角”
两大拇指代表被截直线，食指代表截线
下列三幅图依次表示 
A. 同位角、同旁内角、内错角B. 同位角、内错角、同旁内角
C. 同位角、对顶角、同旁内角D. 同位角、内错角、对顶角
参考答案：
【答案】B
【解析】
两条线a、b被第三条直线c所截,在截线的同旁,被截两直线的同一方,把这种位置关系的角称为同位角;两个角分别在截线的异侧,且夹在两条被截线之间,具有这样位置关系的一对角互为内错角;两个角都在截线的同一侧,且在两条被截线之间,具有这样位置关系的一对角互为同旁内角,据此作答即可.
解:根据同位角、内错角、同旁内角的概念,可知
第一个图是同位角,第二个图是内错角,第三个图是同旁内角.
所以B选项是正确的,
-
科目： 来源： 题型：
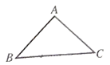
查看答案和解析>>【题目】如图,△ABC是等腰直角三角形,∠A=90°，BC=4.
（1）建立适当的平面直角坐标系,写出各个顶点的坐标；
（2）将△ABC向左平移5个单位,请在图中画出平移后的△A1B1C1；
（3）将△A1B1C1绕点C1按逆时针旋转90°，请在图中画出旋转后的△A2B2C1.
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图1，在∠A内部有一点P，连接BP、CP，请回答下列问题：
（1）求证：∠P＝∠1+∠A+∠2；
（2）如图2，利用上面的结论，在五角星中，∠A+∠B+∠C+∠D+∠E＝ ；
（3）如图3，如果在∠BAC间有两个向上突起的角，请你根据前面的结论猜想∠1、∠2、∠3、∠4、∠5、∠A之间有什么等量关系，直接写出结论即可．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图1，已知直角梯形ABCO中，∠AOC＝90°，AB∥x轴，AB＝6，若以O为原点，OA，OC所在直线为y轴和x轴建立如图所示直角坐标系，A(0，a)，C(c，0)中a，c满足|a+c﹣1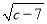0|+
＝0（1）求出点A、B、C的坐标；
（2）如图2，若点M从点C出发，以2单位/秒的速度沿CO方向移动，点N从原点出发，以1单位/秒的速度沿OA方向移动，设M、N两点同时出发，且运动时间为t秒，当点N从点O运动到点A时，点M同时也停止运动，在它们的移动过程中，当2S△ABN≤S△BCM时，求t的取值范围：
（3）如图3，若点N是线段OA延长上的一动点，∠NCH＝k∠OCH，∠CNQ＝k∠BNQ，其中k＞1，NQ∥CJ，求
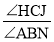的值（结果用含k的式子表示）．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在平面直角坐标系xOy中，已知正比例函数y＝
x的图象与反比例函数y＝
的图象交于A（a，－2），B两点．（1）求反比例函数的表达式和点B的坐标；
（2）P是第一象限内反比例函数图象上一点，过点P作y轴的平行线，交直线AB于点C，连接PO，若△POC的面积为3，求点P的坐标．
-
科目： 来源： 题型：
查看答案和解析>>【题目】（1）如图，
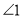与
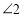是直线________和________被直线________所截得的________角.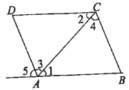
（2）
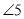与
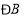是直线________和________被直线________所截得的________角.（3）
与
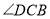是直线________和________被直线________所截得的________角. -
科目： 来源： 题型：
查看答案和解析>>【题目】已知：如图是一个跳棋棋盘，其游戏规则是一个棋子从某一个起始角开始，经过若干步跳动以后，到达终点角跳动时，每一步只能跳到它的同位角或内错角或同旁内角的位置上例如：从起始位置
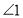跳到终点位置
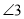有两种不同路径，路径1：
；路径2：
.
试一试：（1）写出从起始位置
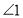跳到终点位置
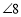的一种路径；（2）从起始位置
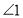依次按同位角、内错角、同旁内角的顺序跳，能否跳到终点位置？
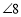相关试题
