【题目】一名足球守门员练习折返跑,从球门的位置出发,向前记作正数,返回记作负数,他的记录如下(单位:米):
+6 | - 5 | +9 | - 10 | +13 | - 9 | - 4. |
(1)守门员是否回到了原来的位置?
(2)守门员离开球门的位置最远是多少?
(3)守门员一共走了多少路程?
参考答案:
【答案】(1)回到了原来的位置;(2)13米;(3)56米.
【解析】
(1)只需将所有数加起来,看其和是否为0即可;
(2)计算每一次跑后的数据,绝对值最大的即为所求;
(3)将所有绝对值相加即可.
解:(1)根据题意得:6-5+9-10+13-9-4=0.
答:回到了原来的位置.
(2)第一次离开6米,第二次离开6-5=1米,第三次离开1+9=10米,第四次离开10-10=0米,第五次离开0+13=13米,第六次离开13-9=4米,第七次离开4-4=0米,
则守门员离开守门的位置最远是13米;
(3)总路程=![]() =56米.
=56米.
故答案为:(1)回到了原来的位置;(2)13米;(3)56米.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠ACB=90°,AC=3,BC=4,过点B作射线BB1∥AC.动点D从点A出发沿射线AC方向以每秒5个单位的速度运动,同时动点E从点C沿射线AC方向以每秒3个单位的速度运动.过点D作DH⊥AB于H,过点E作EF⊥AC交射线BB1于F,G是EF中点,连接DG.设点D运动的时间为t秒.
(1)当t为何值时,AD=AB,并求出此时DE的长度;
(2)当△DEG与△ACB相似时,求t的值.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知如图,在菱形ABCD中,对角线AC、BD相交于点O,DE∥AC,AE∥BD.

(1)求证:四边形AODE是矩形;
(2)若AB=12,∠BCD=120°,求四边形AODE的面积
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,放置的
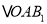 ,
,  ,
, 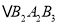 ,…都是边长为2的等边三角形,边
,…都是边长为2的等边三角形,边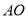 在
在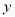 轴上,点
轴上,点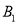 ,
, 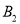 ,
, 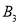 ,…都在直线
,…都在直线 上,则
上,则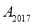 的坐标是( )
的坐标是( )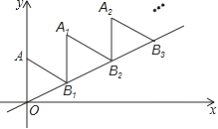
A. (2017,2017
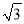 ) B. (2017
) B. (2017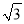 ,2017)
,2017)C. (2017,2018) D. (2017
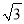 ,2019)
,2019) -
科目: 来源: 题型:
查看答案和解析>>【题目】我们知道,假分数可以化为整数与真分数的和的形式.例如:
 .在分式中,对于只含有一个字母的分式,当分子的次数大于或等于分母的次数时,我们称之为“假分式”;当分子的次数小于分母的次数时,我们称之为“真分式”.例如:像
.在分式中,对于只含有一个字母的分式,当分子的次数大于或等于分母的次数时,我们称之为“假分式”;当分子的次数小于分母的次数时,我们称之为“真分式”.例如:像 ,
, ,…这样的分式是假分式;像
,…这样的分式是假分式;像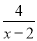 ,
, ,…这样的分式是真分式.类似的,假分式也可以化为整式与真分式的和的形式. 例如:
,…这样的分式是真分式.类似的,假分式也可以化为整式与真分式的和的形式. 例如:  ’
’ .
.(1)将分式
 化为整式与真分式的和的形式;
化为整式与真分式的和的形式;(2)如果分式
 的值为整数,求x的整数值.
的值为整数,求x的整数值. -
科目: 来源: 题型:
查看答案和解析>>【题目】先阅读下列材料,再解决问题:
学习数轴之后,有同学发现在数轴上到两点之间距离相等的点,可以用表示这两点表示的数来确定.如:(1)到表示数4和数10距离相等的点表示的数是7,有这样的关系7=
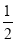 (4+10);
(4+10); (2)到表示数-3和数-7距离相等的点表示的数是-5,有这样的关系-5=
 .
.解决问题:根据上述规律完成下列各题:
(1)到表示数50和数150距离相等的点表示的数是_________
(2)到表示数
 和数
和数 距离相等的点表示的数是__________
距离相等的点表示的数是__________ (3)到表示数
 12和数
12和数 26距离相等的点表示的数是_________
26距离相等的点表示的数是_________ (4)到表示数a和数b距离相等的点表示的数是___________
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图A在数轴上对应的数为-2.
(1)点B在点A右边距离A点4个单位长度,则点B所对应的数是_____.
(2)在(1)的条件下,点A以每秒2个单位长度沿数轴向左运动,点B以每秒3个单位长度沿数轴向右运动.现两点同时运动,当点A运动到-6的点处时,求A、B两点间的距离.
(3)在(2)的条件下,现A点静止不动,B点以原速沿数轴向左运动,经过多长时间A、B两点相距4个单位长度.

相关试题

