【题目】如图,在Rt△ABC中,∠ACB=90°,AC=3,BC=4,过点B作射线BB1∥AC.动点D从点A出发沿射线AC方向以每秒5个单位的速度运动,同时动点E从点C沿射线AC方向以每秒3个单位的速度运动.过点D作DH⊥AB于H,过点E作EF⊥AC交射线BB1于F,G是EF中点,连接DG.设点D运动的时间为t秒.
(1)当t为何值时,AD=AB,并求出此时DE的长度;
(2)当△DEG与△ACB相似时,求t的值.

参考答案:
【答案】(1)当t=1时,AD=AB,AE=1;
(2)当t=![]() 或
或 ![]() 或
或 ![]() 或
或 ![]() 时,△DEG与△ACB相似.
时,△DEG与△ACB相似.
【解析】试题分析:(1)根据勾股定理得出AB=5,要使AD=AB=5,∵动点D每秒5个单位的速度运动,∴t=1;(2)当△DEG与△ACB相似时,要分两种情况讨论,根据相似三角形的性质,列出比例式,求出DE的表达式时,要分AD<AE和AD>AE两种情况讨论.
试题解析:
(1)∵∠ACB=90°,AC=3,BC=4, ∴AB=![]() =5.
=5.
∵AD=5t,CE=3t, ∴当AD=AB时,5t=5,即t=1;
∴AE=AC+CE=3+3t=6,DE=6﹣5=1.
(2)∵EF=BC=4,G是EF的中点, ∴GE=2.
当AD<AE(即t<![]() )时,DE=AE﹣AD=3+3t﹣5t=3﹣2t,
)时,DE=AE﹣AD=3+3t﹣5t=3﹣2t,
若△DEG与△ACB相似,则 ![]() 或
或 ![]() ,
,
∴![]() 或
或![]() , ∴t=
, ∴t=![]() 或t=
或t=![]() ;
;
当AD>AE(即t>![]() )时,DE=AD﹣AE=5t﹣(3+3t)=2t﹣3,
)时,DE=AD﹣AE=5t﹣(3+3t)=2t﹣3,
若△DEG与△ACB相似,则 ![]() 或
或 ![]() , ∴
, ∴![]() 或
或![]() ,
,
解得t=![]() 或t=
或t=![]() ;
;
综上所述,当t=![]() 或
或 ![]() 或
或 ![]() 或
或 ![]() 时,△DEG与△ACB相似.
时,△DEG与△ACB相似.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:
(1)
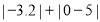 -
-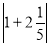 ;
;(2)0

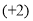



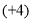

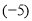
(3)(-
 )-(-
)-(-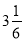 )-(+
)-(+ )+(-
)+(-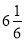 );
);(4)(- 3.125)+(+4.75)+
 +(
+(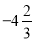 )
) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点
 是正方形
是正方形 对角线
对角线 上一动点,点
上一动点,点 在射线
在射线 上,且
上,且 ,连接
,连接 ,
, 为
为 中点.
中点.(1)如图1,当点
 在线段
在线段 上时,试猜想
上时,试猜想 与
与 的数量关系和位置关系,并说明理由;
的数量关系和位置关系,并说明理由;
(2)如图2,当点
 在线段
在线段 上时,(1)中的猜想还成立吗?请说明理由;
上时,(1)中的猜想还成立吗?请说明理由;
(3)如图3,当点
 在
在 的延长线上时,请你在图3中画出相应的图形,并判断(1)中的猜想是否成立?若成立,请直接写出结论;若不成立,请说明理由.
的延长线上时,请你在图3中画出相应的图形,并判断(1)中的猜想是否成立?若成立,请直接写出结论;若不成立,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知直线y=k1x+b与x轴、y轴相交于P,Q两点,与y=
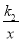 的图象相交于A(-2,m),B(1,n)两点,连接OA,OB,给出下列论:①k1k2<0;②m+
的图象相交于A(-2,m),B(1,n)两点,连接OA,OB,给出下列论:①k1k2<0;②m+ n=0;③S△AOP=S△BOQ;④不等式k1x+b>
n=0;③S△AOP=S△BOQ;④不等式k1x+b>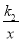 的解集为x<-2或0<x<1.其中正确的结论是________.
的解集为x<-2或0<x<1.其中正确的结论是________.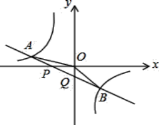
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知如图,在菱形ABCD中,对角线AC、BD相交于点O,DE∥AC,AE∥BD.

(1)求证:四边形AODE是矩形;
(2)若AB=12,∠BCD=120°,求四边形AODE的面积
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,放置的
 ,
,  ,
, 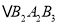 ,…都是边长为2的等边三角形,边
,…都是边长为2的等边三角形,边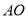 在
在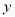 轴上,点
轴上,点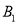 ,
, 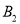 ,
, 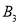 ,…都在直线
,…都在直线 上,则
上,则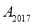 的坐标是( )
的坐标是( )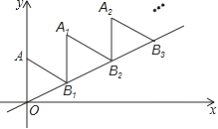
A. (2017,2017
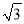 ) B. (2017
) B. (2017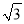 ,2017)
,2017)C. (2017,2018) D. (2017
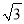 ,2019)
,2019) -
科目: 来源: 题型:
查看答案和解析>>【题目】一名足球守门员练习折返跑,从球门的位置出发,向前记作正数,返回记作负数,他的记录如下(单位:米):
+6
- 5
+9
- 10
+13
- 9
- 4.
(1)守门员是否回到了原来的位置?
(2)守门员离开球门的位置最远是多少?
(3)守门员一共走了多少路程?
相关试题

