【题目】如图,在平面直角坐标系中,过点B(6,0)的直线AB与直线OA相交于点A(4,2),动点M在y轴上运动.
(1)求直线AB的函数解析式;
(2)动点M在y轴上运动,使MA+MB的值最小,求点M的坐标;
(3)在y轴的负半轴上是否存在点M,使△ABM是以AB为直角边的直角三角形?如果存在,求出点M的坐标;如果不存在,说明理由.

参考答案:
【答案】(1)y=-x+6;(2)M(0,![]() );(3)(0,-2)或(0,-6).
);(3)(0,-2)或(0,-6).
【解析】
(1)设AB的函数解析式为:y=kx+b,把A、B两点的坐标代入解方程组即可.
(2)作点B关于y轴的对称点B′,则B′点的坐标为(-6,0),连接AB′则AB′为MA+MB的最小值,根据A、B′两点坐标可知直线AB′的解析式,即可求出M点坐标,(3)分别考虑∠MAB为直角时直线MA的解析式,∠ABM′为直角时直线BM′的解析式,求出M点坐标即可,
(1)设直线AB的函数解析式为y=kx+b,则![]() 解方程组得
解方程组得![]()
直线AB的函数解析式为y= -x+6,
(2)如图作点B关于y轴的对称点B′,则点B′的坐标为(-6,0),连接AB′则AB′为MA+MB的最小值,设直线AB′的解析式为y=mx+n,则![]() ,
,
解方程组得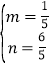
所以直线AB′的解析式为![]() ,
,
当x=0时,y=![]() ,
,
所以M点的坐标为(0,![]() ),
),
(3)有符合条件的点M,理由如下:
如图:因为△ABM是以AB为直角边的直角三角形,
当∠MAB=90°时,直线MA垂直直线AB,
∵直线AB的解析式为y=-x+6,
∴设MA的解析式为y=x+b,
∵点A(4,2),
∴2=4+b,
∴b=-2,
当∠ABM′=90°时,BM′垂直AB,
设BM′的解析式为y=x+n,
∵点B(6,0)
∴6+n=0
∴n=-6,
即有满足条件的点M为(0,-2)或(0,-6).
-
科目: 来源: 题型:
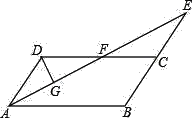
查看答案和解析>>【题目】如图,在平行四边形ABCD中,∠BAD的平分线与BC的延长线交于点E,与DC交于点F.
(1)求证:CD=BE;
(2)若AB=4,点F为DC的中点,DG⊥AE,垂足为G,且DG=1,求AE的长.
-
科目: 来源: 题型:
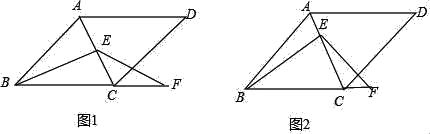
查看答案和解析>>【题目】在菱形ABCD中,∠ABC=60°,E是对角线AC上任意一点,F是线段BC延长线上一点,且CF=AE,连接BE、EF.
(1)如图1,当E是线段AC的中点时,求证:BE=EF.
(2)如图2,当点E不是线段AC的中点,其它条件不变时,请你判断(1)中的结论是否成立?若成立,请证明;若不成立,说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,已知矩形OABC的顶点A在x轴上,OA=4,OC=3,点D为BC边上一点,以AD为一边在与点B的同侧作正方形ADEF,连接OE.当点D在边BC上运动时,OE的长度的最小值是 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】现在,共享单车已遍布深圳街头,其中较为常见的共享单车有“A.摩拜单车”、“B.小蓝单车”、“C.OFO单车”、“D.小鸣单车”、“E.凡骑绿畅”等五种类型.为了解市民使用这些共享单车的情况,某数学兴趣小组随机统计部分正在使用这些单车的市民,并将所得数据绘制出了如下两幅不完整的统计图表 (图1、图2):

根据所给信息解答下列问题:
(1)此次统计的人数为人;根据已知信息补全条形统计图;
(2)在使用单车的类型扇形统计图中,使用E 型共享单车所在的扇形的圆心角为度;
(3)据报道,深圳每天有约200余万人次使用共享单车,则其中使用E型共享单车的约有万人次. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知矩形ABCD 中,E、F 分别为BC、AD 上的点,将四边形ABEF 沿直线EF 折叠后,点B 落在CD 边上的点G 处,点A 的对应点为点H.再将折叠后的图形展开,连接BF、GF、BG,若BF⊥GF.

(1)求证:△ABF≌△DFG;
(2)已知AB=3,AD=5,求tan∠CBG 的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下列材料:
关于x的方程:
 的解是
的解是 ,
, ;
; 即
即 的解是
的解是 ;
; 的解是
的解是 ,
, ;
; 的解是
的解是 ,
, ;
;
 请观察上述方程与解的特征,比较关于x的方程
请观察上述方程与解的特征,比较关于x的方程 与它们的关系,猜想它的解是什么?并利用“方程的解”的概念进行验证.
与它们的关系,猜想它的解是什么?并利用“方程的解”的概念进行验证. 由上述的观察、比较、猜想、验证,可以得出结论:
由上述的观察、比较、猜想、验证,可以得出结论:如果方程的左边是未知数与其倒数的倍数的和,方程的右边的形式与左边完全相同,只是把其中的未知数换成了某个常数,那么这样的方程可以直接得解,请用这个结论解关于x的方程:
 .
.
相关试题

