【题目】现在,共享单车已遍布深圳街头,其中较为常见的共享单车有“A.摩拜单车”、“B.小蓝单车”、“C.OFO单车”、“D.小鸣单车”、“E.凡骑绿畅”等五种类型.为了解市民使用这些共享单车的情况,某数学兴趣小组随机统计部分正在使用这些单车的市民,并将所得数据绘制出了如下两幅不完整的统计图表 (图1、图2):
根据所给信息解答下列问题:
(1)此次统计的人数为人;根据已知信息补全条形统计图;
(2)在使用单车的类型扇形统计图中,使用E 型共享单车所在的扇形的圆心角为度;
(3)据报道,深圳每天有约200余万人次使用共享单车,则其中使用E型共享单车的约有万人次.
参考答案:
【答案】
(1)300
(2)64.8
(3)36
【解析】解:(1.)根据题意得:75÷25%=300(人),补全条形统计图,如下图: 
(2.)根据题意得:54÷300×360°=64.8°,
则使用E 型共享单车所在的扇形的圆心角为64.8度;
(3.)根据题意得: ![]() ×200=36(万人),
×200=36(万人),
则其中使用E型共享单车的约有36万人,
所以答案是:(1)300;(2)64.8;(3)36
【考点精析】本题主要考查了扇形统计图和条形统计图的相关知识点,需要掌握能清楚地表示出各部分在总体中所占的百分比.但是不能清楚地表示出每个项目的具体数目以及事物的变化情况;能清楚地表示出每个项目的具体数目,但是不能清楚地表示出各个部分在总体中所占的百分比以及事物的变化情况才能正确解答此题.
-
科目: 来源: 题型:
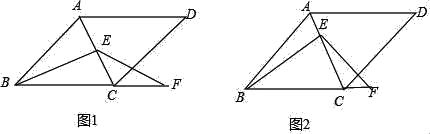
查看答案和解析>>【题目】在菱形ABCD中,∠ABC=60°,E是对角线AC上任意一点,F是线段BC延长线上一点,且CF=AE,连接BE、EF.
(1)如图1,当E是线段AC的中点时,求证:BE=EF.
(2)如图2,当点E不是线段AC的中点,其它条件不变时,请你判断(1)中的结论是否成立?若成立,请证明;若不成立,说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,已知矩形OABC的顶点A在x轴上,OA=4,OC=3,点D为BC边上一点,以AD为一边在与点B的同侧作正方形ADEF,连接OE.当点D在边BC上运动时,OE的长度的最小值是 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,过点B(6,0)的直线AB与直线OA相交于点A(4,2),动点M在y轴上运动.
(1)求直线AB的函数解析式;
(2)动点M在y轴上运动,使MA+MB的值最小,求点M的坐标;
(3)在y轴的负半轴上是否存在点M,使△ABM是以AB为直角边的直角三角形?如果存在,求出点M的坐标;如果不存在,说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知矩形ABCD 中,E、F 分别为BC、AD 上的点,将四边形ABEF 沿直线EF 折叠后,点B 落在CD 边上的点G 处,点A 的对应点为点H.再将折叠后的图形展开,连接BF、GF、BG,若BF⊥GF.

(1)求证:△ABF≌△DFG;
(2)已知AB=3,AD=5,求tan∠CBG 的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下列材料:
关于x的方程:
 的解是
的解是 ,
, ;
; 即
即 的解是
的解是 ;
; 的解是
的解是 ,
, ;
; 的解是
的解是 ,
, ;
;
 请观察上述方程与解的特征,比较关于x的方程
请观察上述方程与解的特征,比较关于x的方程 与它们的关系,猜想它的解是什么?并利用“方程的解”的概念进行验证.
与它们的关系,猜想它的解是什么?并利用“方程的解”的概念进行验证. 由上述的观察、比较、猜想、验证,可以得出结论:
由上述的观察、比较、猜想、验证,可以得出结论:如果方程的左边是未知数与其倒数的倍数的和,方程的右边的形式与左边完全相同,只是把其中的未知数换成了某个常数,那么这样的方程可以直接得解,请用这个结论解关于x的方程:
 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】某电器商场销售甲、乙两种品牌空调,已知每台乙种品牌空调的进价比每台甲种品牌空调的进价高20%,用7200元购进的乙种品牌空调数量比用3000元购进的甲种品牌空调数量多2 台.
(1)求甲、乙两种品牌空调的进货价;
(2)该商场拟用不超过16000 元购进甲、乙两种品牌空调共10台进行销售,其中甲种品牌空调的售价为2500元/台,乙种品牌空调的售价为3500元/台.请你帮该商场设计一种进货方案,使得在售完这10 台空调后获利最大,并求出最大利润.
相关试题

