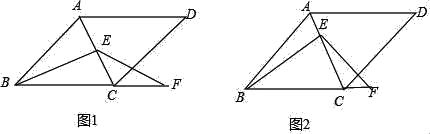
【题目】在菱形ABCD中,∠ABC=60°,E是对角线AC上任意一点,F是线段BC延长线上一点,且CF=AE,连接BE、EF.
(1)如图1,当E是线段AC的中点时,求证:BE=EF.
(2)如图2,当点E不是线段AC的中点,其它条件不变时,请你判断(1)中的结论是否成立?若成立,请证明;若不成立,说明理由.
参考答案:
【答案】(1)详见解析;(2)结论成立,理由详见解析.
【解析】
(1)由四边形ABCD是菱形,∠ABC=60°,可知△ABC是等边三角形,因为E是线段AC的中点,所以∠CBE=∠ABE=30°,AE=CE,由AE=CF得CE=CF可知∠CEF=∠F由∠ACF=120°可知∠F=30°∴∠F=∠CBE=30°。即可证明BE=EF.(2)过点E作EG∥BC交AB于点G,可得∠AGE=∠ABC=60°,因为∠BAC=60°,所以△AGE是等边三角形,可知AG=AE=GE,∠AGE=60°,可知BG=CE,因为CF=AE,所以GE=CF,进而可证明△BGE≌△ECF,即可证明BE=EF.
(1)∵四边形ABCD是菱形,
∴AB=BC,
∵∠ABC=60°,
∴△ABC是等边三角形,
∴∠BCA=60°,
∵E是线段AC的中点,
∴∠CBE=∠ABE=30°,AE=CE,
∵CF=AE,
∴CE=CF,
∵∠ECF=120°,
∴∠F=∠CEF=30°
∴∠CBE=∠F=30°,
∴BE=EF;
(2)结论成立;理由如下:
过点E作EG∥BC交AB于点G,如图2所示:
∵四边形ABCD为菱形,
∴AB=BC,∠BCD=120°,AB∥CD,
∴∠ACD=60°,∠DCF=∠ABC=60°,
∴∠ECF=120°,
又∵∠ABC=60°,
∴△ABC是等边三角形,
∴AB=AC,∠ACB=60°,
又∵EG∥BC,
∴∠AGE=∠ABC=60°,
又∵∠BAC=60°,
∴△AGE是等边三角形,
∴AG=AE=GE,∠AGE=60°,
∴BG=CE,,
又∵CF=AE,
∴GE=CF,
∵在△BGE和△CEF中,BG=CE,∠BGE=∠ECF,GE=CF,
∴△BGE≌△ECF(SAS),
∴BE=EF.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形ABCD中,AB=2,BC=4,P为矩形边上的一个动点,运动路线是A→B→C→D→A,设P点经过的路程为x,以A,P,B为顶点的三角形面积为y,则选项图象能大致反映y与x的函数关系的是( )
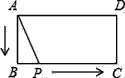
A.
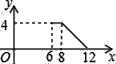 B.
B. 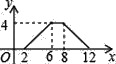 C.
C. 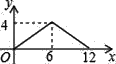 D.
D. 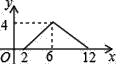
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,甲、乙两人以相同路线前往离学校12千米的地方参加植树活动.分析甲、乙两人前往目的地所行驶的路程S(千米)随时间t(分钟)变化的函数图象,解决下列问题:
(1)求出甲、乙两人所行驶的路程S甲、S乙与t之间的关系式;
(2)甲行驶10分钟后,甲、乙两人相距多少千米?

-
科目: 来源: 题型:
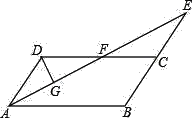
查看答案和解析>>【题目】如图,在平行四边形ABCD中,∠BAD的平分线与BC的延长线交于点E,与DC交于点F.
(1)求证:CD=BE;
(2)若AB=4,点F为DC的中点,DG⊥AE,垂足为G,且DG=1,求AE的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,已知矩形OABC的顶点A在x轴上,OA=4,OC=3,点D为BC边上一点,以AD为一边在与点B的同侧作正方形ADEF,连接OE.当点D在边BC上运动时,OE的长度的最小值是 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,过点B(6,0)的直线AB与直线OA相交于点A(4,2),动点M在y轴上运动.
(1)求直线AB的函数解析式;
(2)动点M在y轴上运动,使MA+MB的值最小,求点M的坐标;
(3)在y轴的负半轴上是否存在点M,使△ABM是以AB为直角边的直角三角形?如果存在,求出点M的坐标;如果不存在,说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】现在,共享单车已遍布深圳街头,其中较为常见的共享单车有“A.摩拜单车”、“B.小蓝单车”、“C.OFO单车”、“D.小鸣单车”、“E.凡骑绿畅”等五种类型.为了解市民使用这些共享单车的情况,某数学兴趣小组随机统计部分正在使用这些单车的市民,并将所得数据绘制出了如下两幅不完整的统计图表 (图1、图2):

根据所给信息解答下列问题:
(1)此次统计的人数为人;根据已知信息补全条形统计图;
(2)在使用单车的类型扇形统计图中,使用E 型共享单车所在的扇形的圆心角为度;
(3)据报道,深圳每天有约200余万人次使用共享单车,则其中使用E型共享单车的约有万人次.
相关试题

