【题目】如图,点P在射线AB的上方,且∠PAB=45°,PA=2,点M是射线AB上的动点(点M不与点A重合),现将点P绕点A按顺时针方向旋转60°到点Q,将点M绕点P按逆时针方向旋转60°到点N,连接AQ,PM,PN,作直线QN.
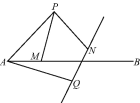
(1)求证:AM=QN.
(2)直线QN与以点P为圆心,以PN的长为半径的圆是否存在相切的情况?若存在,请求出此时AM的长,若不存在,请说明理由.
(3)当以点P为圆心,以PN的长为半径的圆经过点Q时,直接写出劣弧NQ与两条半径所围成的扇形的面积.
参考答案:
【答案】(1)证明见解析; (2)存在.理由见解析; (3)劣弧NQ与两条半径所围成的扇形的面积为π.
【解析】
(1)根据旋转的旋转判断出△APQ为等边三角形,再判断出∠APM=∠QPN,从而得出△APM≌△QPN即可;
(2)由直线和圆相切得出∠AMP=∠QNP=90°,再用勾股定理即可求出结论;
(3)先判断出PA=PQ,再判断出PQ=PN=PM,进而求出∠QPM=30°,即可求出∠QPN=90°,最后用扇形的面积公式即可.
(1)如图1,连接PQ,由点P绕点A按顺时针方向旋转60°到点Q,
可得AP=AQ,∠PAQ=60°,
∴△APQ为等边三角形,
∴PA=PQ,∠APQ=60°,
由点M绕点P按逆时针方向旋转60°到点N,
可得PM=PN,∠MPN=60°,
∴∠APM=∠QPN,则△APM≌△QPN(SAS),
∴AM=QN.
(2)存在.理由如下:
如图2,由(1)中的证明可知△APM≌△QPN,
∴∠AMP=∠QNP,
∵直线QN与以点P为圆心,以PN的长为半径的圆相切,
∴∠AMP=∠QNP=90°,即PN⊥QN.
在Rt△APM中,∠PAB=45°,PA=2,
∴AM=![]() .
.
(3)由(1)知△APQ是等边三角形,
∴PA=PQ,∠APQ=60°.
∵以点P为圆心,以PN的长为半径的圆经过点Q,
∴PN=PQ=PA.
∵PM=PN,
∴PA=PM,
∵∠PAB=45°,
∴∠APM=90°,
∴∠MPQ=∠APM-∠APQ=30°.
∵∠MPN=60°,
∴∠QPN=90°,
∴劣弧NQ与两条半径所围成的扇形的面积是扇形QPN的面积,而此扇形的圆心角∠QPN=90°,半径为PN=PM=PA=2.
∴劣弧NQ与两条半径所围成的扇形的面积=![]() =π.
=π.
-
科目: 来源: 题型:
查看答案和解析>>【题目】随着经济的快速发展,环境问题越来越受到人们的关注.某校学生会为了了解垃圾分类知识的普及情况,随机调查了部分学生,调查结果分为“非常了解”“了解”“了解较少”“不了解”四类,并将调查结果绘制成下面两幅统计图.

(1)求:本次被调查的学生有多少名?补全条形统计图.
(2)估计该校1200名学生中“非常了解”与“了解”的人数和是多少.
(3)被调查的“非常了解”的学生中有2名男生,其余为女生,从中随机抽取2人在全校做垃圾分类知识交流,请利用画树状图或列表的方法,求恰好抽到一男一女的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形ABCD中,E是AB边的中点,沿EC对折矩形ABCD,使B点落在点P处,折痕为EC,连结AP并延长AP交CD于F点,连结CP并延长CP交AD于Q点.给出以下结论:
①四边形AECF为平行四边形;
②∠PBA=∠APQ;
③△FPC为等腰三角形;
④△APB≌△EPC.
其中正确结论的个数为( )

A. 1 B. 2 C. 3 D. 4
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知∠xOy=90°,线段AB=10,若点A在Oy上滑动,点B随着线段AB在射线Ox上滑动(A,B与O不重合),Rt△AOB的内切圆☉K分别与OA,OB,AB切于点E,F,P.
(1)在上述变化过程中,Rt△AOB的周长,☉K的半径,△AOB外接圆半径,这几个量中不会发生变化的是什么?并简要说明理由.
(2)当AE=4时,求☉K的半径r.
(3)当Rt△AOB的面积为S,AE为x,试求S与x之间的函数关系,并求出S最大时直角边OA的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】王芳将如图所示的三条水平直线m1,m2,m3的其中一条记为x轴(向右为正方向),三条竖直直线m4,m5,m6的其中一条记为y轴(向上为正方向),并在此坐标平面内画出了抛物线y=ax2-6ax-3,则她所选择的x轴和y轴分别为( )
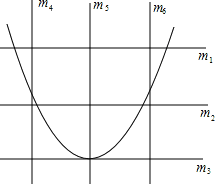
A. m1,m4 B. m2,m3 C. m3,m6 D. m4,m5
-
科目: 来源: 题型:
查看答案和解析>>【题目】在同一平面直角坐标系中,函数y=ax2+b与y=bx2+ax的图象可能是( )

A. A B. B C. C D. D
-
科目: 来源: 题型:
查看答案和解析>>【题目】小王是“新星厂”的一名工人,请你阅读下列信息:
信息一:工人工作时间:每天上午8:00—12:00,下午14:00—18:00,每月工作25天;
信息二:小王生产甲、乙两种产品的件数与所用时间的关系见下表:
生产甲种产品数(件)
生产乙种产品数(件)
所用时间(分钟)
10
10
350
30
20
850
信息三:按件计酬,每生产一件甲种产品得1.50元,每生产一件乙种产品得2.80元;
信息四:该厂工人每月收入由底薪和计酬工资两部分构成,小王每月的底薪为1900元.请根据以上信息,解答下列问题:
(1)小王每生产一件甲种产品和一件乙种产品分别需要多少分钟;
(2)2018年1月工厂要求小王生产甲种产品的件数不少于60件,则小王该月收入最多是多少元?此时小王生产的甲、乙两种产品分别是多少件?
相关试题

