【题目】如图,在矩形ABCD中,E是AB边的中点,沿EC对折矩形ABCD,使B点落在点P处,折痕为EC,连结AP并延长AP交CD于F点,连结CP并延长CP交AD于Q点.给出以下结论:
①四边形AECF为平行四边形;
②∠PBA=∠APQ;
③△FPC为等腰三角形;
④△APB≌△EPC.
其中正确结论的个数为( )

A. 1 B. 2 C. 3 D. 4
参考答案:
【答案】B
【解析】①根据三角形内角和为180°易证∠PAB+∠PBA=90°,易证四边形AECF是平行四边形,即可解题;
②根据平角定义得:∠APQ+∠BPC=90°,由正方形可知每个内角都是直角,再由同角的余角相等,即可解题;
③根据平行线和翻折的性质得:∠FPC=∠PCE=∠BCE,∠FPC≠∠FCP,且∠PFC是钝角,△FPC不一定为等腰三角形;
④当BP=AD或△BPC是等边三角形时,△APB≌△FDA,即可解题.
①如图,EC,BP交于点G;
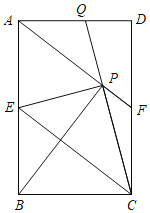
∵点P是点B关于直线EC的对称点,
∴EC垂直平分BP,
∴EP=EB,
∴∠EBP=∠EPB,
∵点E为AB中点,
∴AE=EB,
∴AE=EP,
∴∠PAB=∠PBA,
∵∠PAB+∠PBA+∠APB=180°,即∠PAB+∠PBA+∠APE+∠BPE=2(∠PAB+∠PBA)=180°,
∴∠PAB+∠PBA=90°,
∴AP⊥BP,
∴AF∥EC;
∵AE∥CF,
∴四边形AECF是平行四边形,
故①正确;
②∵∠APB=90°,
∴∠APQ+∠BPC=90°,
由折叠得:BC=PC,
∴∠BPC=∠PBC,
∵四边形ABCD是正方形,
∴∠ABC=∠ABP+∠PBC=90°,
∴∠ABP=∠APQ,
故②正确;
③∵AF∥EC,
∴∠FPC=∠PCE=∠BCE,
∵∠PFC是钝角,
当△BPC是等边三角形,即∠BCE=30°时,才有∠FPC=∠FCP,
如右图,△PCF不一定是等腰三角形,
故③不正确;
④∵AF=EC,AD=BC=PC,∠ADF=∠EPC=90°,
∴Rt△EPC≌△FDA(HL),
∵∠ADF=∠APB=90°,∠FAD=∠ABP,
当BP=AD或△BPC是等边三角形时,△APB≌△FDA,
∴△APB≌△EPC,
故④不正确;
其中正确结论有①②,2个,
故选:B.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,梯形
 中,上底
中,上底 下底
下底 高
高 梯形的面积
梯形的面积 动点
动点 从点
从点 出发,沿
出发,沿 方向,以每秒
方向,以每秒 个单位长度的速度匀速运动.
个单位长度的速度匀速运动.
 请根据
请根据 与
与 的关系式,完成下列问题:
的关系式,完成下列问题:




···





···
 补充表格中的数据;
补充表格中的数据;  当
当 时,表示的图形是_ .
时,表示的图形是_ . 梯形的面积
梯形的面积 与
与 的关系如图2所示,则点
的关系如图2所示,则点 表示的实际意义是_ ;
表示的实际意义是_ ;
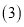 若点
若点 运动的时间为
运动的时间为 的面积为
的面积为 与
与 的关系如图3所示.求
的关系如图3所示.求 的长和
的长和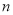 的值.
的值.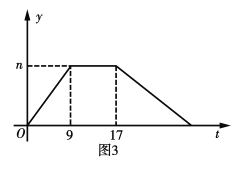
-
科目: 来源: 题型:
查看答案和解析>>【题目】在等边三角形
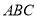 中
中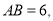 点
点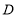 是
是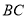 边上的一点,点
边上的一点,点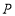 是
是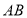 边上的一点,连接
边上的一点,连接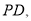 以
以 为边作等边三角形
为边作等边三角形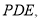 连接
连接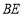 .
.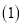 如图1,当点
如图1,当点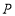 与点
与点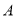 重合时,
重合时,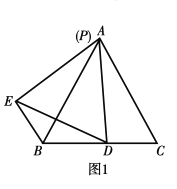
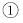 找出图中的一对全等三角形,并证明;
找出图中的一对全等三角形,并证明;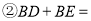 ;
; 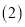 如图2,若
如图2,若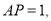 请计算
请计算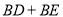 的值.
的值.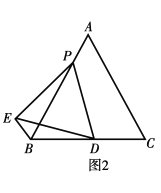
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在△ABO中,∠OAB=90°,∠AOB=30°,OB=8.以OB为一边,在△OAB外作等边三角形OBC,D是OB的中点,连接AD并延长交OC于E.
(1)求点B的坐标;
(2)求证:四边形ABCE是平行四边形;
(3)如图2,将图1中的四边形ABCO折叠,使点C与点A重合,折痕为FG,求OG的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在长方形ABCD中,AB=3,BC=4,动点P从点A开始按A→B→C→D的方向运动到点D.如图,设动点P所经过的路程为x,△APD的面积为y.(当点P与点A或D重合时,y=0)
(1)写出y与x之间的函数解析式;
(2)画出此函数的图象.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形ABCD中,AB=4,AD=3,矩形内部有一动点P满足S△PAB=
 S矩形ABCD,则点P到A、B两点的距离之和PA+PB的最小值为______.
S矩形ABCD,则点P到A、B两点的距离之和PA+PB的最小值为______.
-
科目: 来源: 题型:
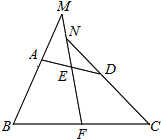
查看答案和解析>>【题目】如图,在四边形ABCD中,E、F分别是AD、BC的中点,连接FE并延长,分别交CD的延长线于点M、N,∠BME=∠CNE,求证:AB=CD.
相关试题

