【题目】小王是“新星厂”的一名工人,请你阅读下列信息:
信息一:工人工作时间:每天上午8:00—12:00,下午14:00—18:00,每月工作25天;
信息二:小王生产甲、乙两种产品的件数与所用时间的关系见下表:
生产甲种产品数(件) | 生产乙种产品数(件) | 所用时间(分钟) |
10 | 10 | 350 |
30 | 20 | 850 |
信息三:按件计酬,每生产一件甲种产品得1.50元,每生产一件乙种产品得2.80元;
信息四:该厂工人每月收入由底薪和计酬工资两部分构成,小王每月的底薪为1900元.请根据以上信息,解答下列问题:
(1)小王每生产一件甲种产品和一件乙种产品分别需要多少分钟;
(2)2018年1月工厂要求小王生产甲种产品的件数不少于60件,则小王该月收入最多是多少元?此时小王生产的甲、乙两种产品分别是多少件?
参考答案:
【答案】(1)生产一件甲产品需要15分,生产一件乙产品需要20分;(2)小王该月最多能得3544元,此时生产甲、乙两种产品分别60,555件.
【解析】
(1)根据图表列出二元一次方程组即可求解,(2)根据甲乙生产时间的关系,表示出生产乙种产品用时,进而表示出甲乙生产数量,可得总利润关系式,讨论即可求解.
(1)设生产一件甲种产品需x分,生产一件乙种产品需y分.
由题意得:![]() ,
,
解这个方程组得:![]() ,
,
答:生产一件甲产品需要15分,生产一件乙产品需要20分.
(2)设生产甲种产品共用x分,则生产乙种产品用(25×8×60-x)分.
则生产甲种产品![]() 件,生产乙种产品
件,生产乙种产品![]() 件.
件.
∴w总额=1.5×![]() +2.8×
+2.8×![]()
=0.1x+![]() ×2.8
×2.8
=0.1x+1680-0.14x
=-0.04x+1680,
又![]() ≥60,得x≥900,
≥60,得x≥900,
由一次函数的增减性,当x=900时w取得最大值,此时w=0.04×900+1680=1644(元),
则小王该月收入最多是1644+1900=3544(元),
此时甲有![]() =60(件),
=60(件),
乙有:![]() =555(件),
=555(件),
答:小王该月最多能得3544元,此时生产甲、乙两种产品分别60,555件.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点P在射线AB的上方,且∠PAB=45°,PA=2,点M是射线AB上的动点(点M不与点A重合),现将点P绕点A按顺时针方向旋转60°到点Q,将点M绕点P按逆时针方向旋转60°到点N,连接AQ,PM,PN,作直线QN.
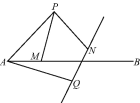
(1)求证:AM=QN.
(2)直线QN与以点P为圆心,以PN的长为半径的圆是否存在相切的情况?若存在,请求出此时AM的长,若不存在,请说明理由.
(3)当以点P为圆心,以PN的长为半径的圆经过点Q时,直接写出劣弧NQ与两条半径所围成的扇形的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】王芳将如图所示的三条水平直线m1,m2,m3的其中一条记为x轴(向右为正方向),三条竖直直线m4,m5,m6的其中一条记为y轴(向上为正方向),并在此坐标平面内画出了抛物线y=ax2-6ax-3,则她所选择的x轴和y轴分别为( )
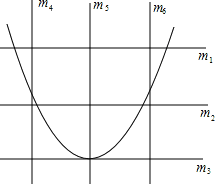
A. m1,m4 B. m2,m3 C. m3,m6 D. m4,m5
-
科目: 来源: 题型:
查看答案和解析>>【题目】在同一平面直角坐标系中,函数y=ax2+b与y=bx2+ax的图象可能是( )

A. A B. B C. C D. D
-
科目: 来源: 题型:
查看答案和解析>>【题目】正方形
 的边长为1,点
的边长为1,点 是
是 边上的一个动点(与
边上的一个动点(与 ,
, 不重合),以
不重合),以 为顶点在
为顶点在 所在直线的上方作
所在直线的上方作
(1)当
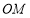 经过点
经过点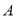 时,
时,①请直接填空:
 ________(可能,不可能)过
________(可能,不可能)过 点:(图1仅供分析)
点:(图1仅供分析)②如图2,在
 上截取
上截取 ,过
,过 点作
点作 垂直于直线
垂直于直线 ,垂足为点
,垂足为点 ,作
,作 于
于 ,求证:四边形
,求证:四边形 为正方形;
为正方形;③如图2,将②中的已知与结论互换,即在
 上取点
上取点 (
( 点在正方形
点在正方形 外部),过
外部),过 点作
点作 垂直于直线
垂直于直线 ,垂足为点
,垂足为点 ,作
,作 于
于 ,若四边形
,若四边形 为正方形,那么
为正方形,那么 与
与 是否相等?请说明理由;
是否相等?请说明理由;(2)当点
 在射线
在射线 上且
上且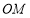 不过点
不过点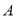 时,设
时,设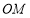 交边
交边 于
于 ,且
,且 .在
.在 上存在点
上存在点 ,过
,过 点作
点作 垂直于直线
垂直于直线 ,垂足为点
,垂足为点 ,使得
,使得 ,连接
,连接 ,则当
,则当 为何值时,四边形
为何值时,四边形 的面积最大?最大面积为多少?
的面积最大?最大面积为多少?


-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在正方形ABCD中,AB=3,点E,F分别在CD,AD上,CE=DF,BE,CF相交于点G.若图中阴影部分的面积与正方形ABCD的面积之比为2:3,则△BCG的周长为_____.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,关于x的二次函数y=ax2﹣2ax(a>0)的顶点为C,与x轴交于点O、A,关于x的一次函数y=﹣ax(a>0).
(1)试说明点C在一次函数的图象上;
(2)若两个点(k,y1)、(k+2,y2)(k≠0,±2)都在二次函数的图象上,是否存在整数k,满足
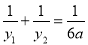 ?如果存在,请求出k的值;如果不存在,请说明理由;
?如果存在,请求出k的值;如果不存在,请说明理由;(3)若点E是二次函数图象上一动点,E点的横坐标是n,且﹣1≤n≤1,过点E作y轴的平行线,与一次函数图象交于点F,当0<a≤2时,求线段EF的最大值.
相关试题

