【题目】(观察发现):(1)如图1,四边形ABCD和四边形AEFG都是正方形,且点E在边AB上,连接DE和BG,猜想线段DE与BG的数量关系和位置关系.(只要求写出结论,不必说出理由)
(深入探究):(2)如图2,将图1中正方形AEFG绕点A逆时针旋转一定的角度,其他条件与观察发现中的条件相同,观察发现中的结论是否还成立?请根据图2加以说明.
(拓展应用):(3)如图3,直线l上有两个动点A、B,直线l外有一点动点Q,连接QA,QB,以线段AB为边在l的另一侧作正方形ABCD,连接QD.随着动点A、B的移动,线段QD的长也会发生变化,若QA,QB长分别为3![]() ,6保持不变,在变化过程中,线段QD的长是否存在最大值?若存在,求出这个最大值;若不存在,请说明理由.
,6保持不变,在变化过程中,线段QD的长是否存在最大值?若存在,求出这个最大值;若不存在,请说明理由.

参考答案:
【答案】(1)DE=BG,DE⊥BG;理由见解析;(2)成立,理由见解析;(3)QD存在最大值为12.
【解析】
观察发现:(1)根据正方形的性质,由SAS证明△BAG≌△DAE,得出DE=BG,∠ABG=∠ADE,再由角的互余关系证出DE⊥BG即可;
深入探究:(2)同(1)证明△BAG≌△DAE,从而证明结论;
拓展应用:(3)以OA为边作正方形QAGF,连接QG、BG,则QG=![]() OA=6,当G、Q、B三点共线时,BG最长,此时BG=QG+QB=12,从而得出答案.
OA=6,当G、Q、B三点共线时,BG最长,此时BG=QG+QB=12,从而得出答案.
(1)DE=BG,DE⊥BG;理由如下:
延长DE交BG于H,如图1所示:
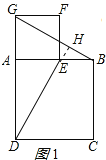
∵四边形ABCD、四边形AEFG都是正方形,
∴AB=AD,AG=AE,∠EAD=∠BAG=90°,
在△BAG与△DAE中,
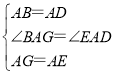 ,
,
∴△BAG≌△DAE(SAS),
∴DE=BG,∠ABG=∠ADE,
∵∠AGB+∠ABG=90°,
∴∠AGB+∠ADE=90°,
∴∠DHG=90°,
∴DE⊥BG;
(2)(1)中的结论成立,即DE=BG,DE⊥BG;
理由如下:如图2所示,
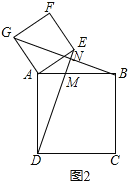
∵四边形ABCD、四边形AEFG都是正方形,
∴BA=AD,AG=AE,∠BAD=∠EAG=90°,
∴∠BAD+∠BAE=∠EAG+∠BAE,
即∠BAG=∠DAE,
在△BAG与△DAE中,
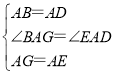 ,
,
∴△BAG≌△DAE(SAS),
∴DE=BG,∠ABG=∠ADE
∵∠AMD+∠ADE=90°,∠AMD=∠BME,
∴∠BME+∠ABG=90°,
∴∠DNB=90°,
∴DE⊥BG;
(3)QD存在最大值;理由如下:
以QA为边作正方形QAGF,连接QG、BG,如图3所示:
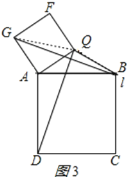
则QG=![]() QA=6,
QA=6,
由(2)可得:QD=BG,
当G、Q、B三点共线时,BG最长,
此时BG=QG+QB=6+6=12,
即线段QD长的最大值为12.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形ABCD中,AB=6,点E在边CD上,且CD=3DE,将△ADE沿AE对折至△AFE,延长EF交边BC于点G,连接AG、CF,

求证:①△ABG≌△AFG;②BG=CG
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列四个函数:①y=﹣
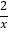 ;②y=2(x+1)2﹣3;③y=﹣2x+5;④y=3x﹣10.其中,当x>﹣1时,y随x的增大而增大的函数是( )
;②y=2(x+1)2﹣3;③y=﹣2x+5;④y=3x﹣10.其中,当x>﹣1时,y随x的增大而增大的函数是( )A. ①④ B. ②③ C. ②④ D. ①②
-
科目: 来源: 题型:
查看答案和解析>>【题目】一元二次方程(x+1)(x﹣2)=10根的情况是( )
A. 无实数根 B. 有两个正根
C. 有两个根,且都大于﹣1 D. 有两个根,其中一根大于2
-
科目: 来源: 题型:
查看答案和解析>>【题目】2010年开始合肥市开展了“体育、艺术2+1”活动,我校根据实际情况,决定主要开设A:乒乓球,B:象棋,C:篮球,D:跳绳这四种运动项目.为了解学生喜欢哪一种项目,随机抽取了部分学生进行调查,并将调查结果绘制成如图甲、乙所示的条形统计图和扇形统计图.请你结合图中的信息解答下列问题:
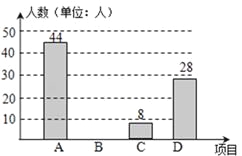

(1)样本中喜欢B项目的人数百分比是 ,其所在扇形统计图中的圆心角的度数是 ;
(2)把条形统计图补充完整;
(3)已知我校有学生2400人,根据样本估计全校喜欢乒乓球的人数是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在正方形ABCD中,O是对角线AC与BD的交点,M是BC边上的动点(点M不与B、C重合),CN⊥DM,CN与AB交于点N,连接OM、ON、MN.下列四个结论:①△CNB≌△DMC;②△CON≌△DOM;③AN2+CM2=MN2;④若AB=2,则S△OMN的最小值是
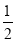 .其中正确结论的个数是( )
.其中正确结论的个数是( )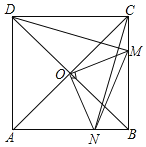
A.1B.2C.3D.4
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形ABCD的边长为2,其面积标记为S1,以CD为斜边作等腰直角三角形,以该等腰直角三角形的一条直角边为边向外作正方形,其面积标记为S2,…按照此规律继续下去,则S2016的值为( )
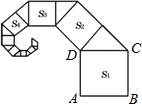
A. (
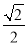 )2013B. (
)2013B. (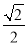 )2014C. (
)2014C. (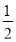 )2013D. (
)2013D. (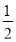 )2014
)2014
相关试题

