【题目】如图,△ABC中,AB=AC=2,∠B=30°,点D在BC上,过点D作DE⊥BC,交BA或其延长线于点E,过点E作EF⊥BA交AC或其延长线于点F,连接DF.若DF⊥AC,则BD=_____.

参考答案:
【答案】![]()
【解析】分析:作AH⊥BC于H,如图,根据等腰三角形的性质得∠C=∠B=30°,BH=CH,再利用三角形外角性质得∠EAF=2∠B=60°,根据含30度角的直角三角形三边的关系得AH=![]() AB=1,BH=
AB=1,BH=![]() AH=
AH=![]() ,所以BC=2BH=2
,所以BC=2BH=2![]() ,同样可得AF=2AE,DF=
,同样可得AF=2AE,DF=![]() CD,CF=
CD,CF=![]() DF=
DF=![]() CD,设BD=x,则CD=2
CD,设BD=x,则CD=2![]() -x,在Rt△BDE中,根据含30度角的直角三角形三边的关系得DE=
-x,在Rt△BDE中,根据含30度角的直角三角形三边的关系得DE=![]() BD=
BD=![]() x,AE=2DE=
x,AE=2DE=![]() x,则AE=BE-AB=
x,则AE=BE-AB=![]() x-2,然后利用x表示出AF=
x-2,然后利用x表示出AF=![]() x-4,CF=
x-4,CF=![]() (2
(2![]() -x),最后利用AF+CF=AC列方程求解.
-x),最后利用AF+CF=AC列方程求解.
详解:作AH⊥BC于H,如图,

∵AB=AC=2,
∴∠C=∠B=30°,BH=CH,
∴∠EAF=2∠B=60°,AH=![]() AB=1,BH=
AB=1,BH=![]() AH=
AH=![]() ,
,
∴BC=2BH=2![]() ,
,
∵EF⊥AB,DF⊥AC,
∴∠AEF=90°,∠DFC=90°,
∴AF=2AE,DF=![]() CD,CF=
CD,CF=![]() DF=
DF=![]() CD,
CD,
设BD=x,则CD=2![]() -x,
-x,
在Rt△BDE中,DE=![]() BD=
BD=![]() x,
x,
∴BE=2DE=![]() x,
x,
∴AE=BE-AB=![]() x-2,
x-2,
∴AF=![]() x-4,CF=
x-4,CF=![]() (2
(2![]() -x),
-x),
∵AF+CF=AC,
∴![]() x-4+
x-4+![]() (2
(2![]() -x)=2,
-x)=2,
解得x=![]() ,
,
即BD的长为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x的方程x2+2kx+k2+k+3=0的两根分别是x1、x2,则(x1﹣1)2+(x2﹣1)2的最小值是_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】大熊山某农家乐为了抓住“五一”小长假的商机,决定购进A、B两种纪念品。若购进A种纪念品4件,B种纪念品3件,需要550元;若购进A种纪念品8件,B种纪念品5件,需要1050元。
(1)求购进A、B两种纪念品每件各需多少元。
(2)若该农家乐决定购进这两种纪念品共100件,考虑市场需求和资金周转,用于购买这100件纪念品的资金不少于7500元,但不超过7650元,那么该农家乐共有几种进货方案。
(3)若销售每件A种纪念品可获利润30元,每件B种纪念品可获利润20元,在第(2)问的各种进货方案中,哪一种方案获利最大?最大利润是多少元。
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图①,
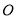 为直线
为直线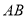 上一点,作射线
上一点,作射线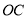 ,使
,使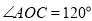 ,将一个直角三角尺如图摆放,直角顶点在点
,将一个直角三角尺如图摆放,直角顶点在点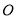 处,一条直角边
处,一条直角边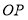 在射线
在射线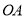 上. 将图
上. 将图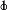 中的三角尺绕点
中的三角尺绕点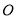 以每秒10°的速度按逆时针方向旋转(如图②所示),在旋转一周的过程中,第
以每秒10°的速度按逆时针方向旋转(如图②所示),在旋转一周的过程中,第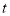 秒时,
秒时,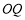 所在直线恰好平分
所在直线恰好平分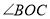 ,则
,则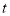 的值为_________.
的值为_________.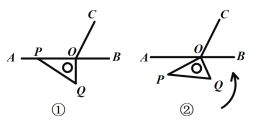
-
科目: 来源: 题型:
查看答案和解析>>【题目】附加题:(y﹣z)2+(x﹣y)2+(z﹣x)2=(y+z﹣2x)2+(z+x﹣2y)2+(x+y﹣2z)2.
求
 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】填空:在横线上填写适当的式,数或符号,完整表达解方程的过程
解方程:
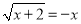 ,
,解:两边平方,得_____________________________________________
整理,得_____________________________________________________
解这个方程得,
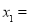 ___________________,
___________________,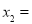 _____________________
_____________________检验:把
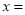 ________分别带入原方程两边,左边=_______________,右边=_________________,由右边__________左边,可知
________分别带入原方程两边,左边=_______________,右边=_________________,由右边__________左边,可知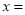 ________是________
________是________把x=_________________分别带入原方程两边,左边=________,左边=_________________右边,可知
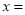 ________是________
________是________所以,原方程的根是___________________________
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,平面内有四个点A,B,C,D. 根据下列语句画图:
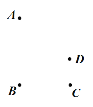
①画直线BC;
②画射线AD交直线
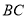 于点E;
于点E;③连接BD,用圆规在线段BD的延长线上截取DF=BD;
④在图中确定点O,使点O到点A,B,C,D的距离之和最小.
(友情提醒:截取用圆规,并保留痕迹;画完图要下结论)
相关试题

