【题目】大熊山某农家乐为了抓住“五一”小长假的商机,决定购进A、B两种纪念品。若购进A种纪念品4件,B种纪念品3件,需要550元;若购进A种纪念品8件,B种纪念品5件,需要1050元。
(1)求购进A、B两种纪念品每件各需多少元。
(2)若该农家乐决定购进这两种纪念品共100件,考虑市场需求和资金周转,用于购买这100件纪念品的资金不少于7500元,但不超过7650元,那么该农家乐共有几种进货方案。
(3)若销售每件A种纪念品可获利润30元,每件B种纪念品可获利润20元,在第(2)问的各种进货方案中,哪一种方案获利最大?最大利润是多少元。
参考答案:
【答案】(1)各需100、50元;(2)四种;(3)购进![]() 种纪念品53件,B种纪念品47件时,获得最大利润是2530元。
种纪念品53件,B种纪念品47件时,获得最大利润是2530元。
【解析】
(1)关系式为:A种纪念品4件需要钱数+B种纪念品3件钱数=550;A种纪念品8件需要钱数+B种纪念品5件需要钱数=1050;
(2)关系式为:用于购买这100件纪念品的资金不少于7500元,但不超过7650元,得出不等式组求出即可;
(3)因为A种纪念品利润较高,故A种数量越多总利润越高,因此选择购A种53件,B种47件.
解:(1)设购进A种纪念品每件需![]() 元,购进B种纪念品每件需
元,购进B种纪念品每件需![]() 元,则根据题意,可列方程组为
元,则根据题意,可列方程组为![]() ,解得
,解得![]() ,则购进A、B两种纪念品每件各需100、50元。
,则购进A、B两种纪念品每件各需100、50元。
(2)设购进A种纪念品![]() 件,购进B种纪念品
件,购进B种纪念品![]() 件,根据题意,可列不等式为
件,根据题意,可列不等式为![]() ,解得
,解得![]() ,因为
,因为![]() 是正整数,所以
是正整数,所以![]() 故有四种方案。①购进A种纪念品50件,B种纪念品50件;
故有四种方案。①购进A种纪念品50件,B种纪念品50件;
②购进A种纪念品51件,B种纪念品49件;
③购进A种纪念品52件,B种纪念品48件;
④购进A种纪念品53件,B种纪念品47件.
(3)设利润为![]() ,则
,则![]() ,则
,则![]() 随
随![]() 的增大而增大,所以
的增大而增大,所以![]() 时,
时,![]() 最大是2530,故购进
最大是2530,故购进![]() 种纪念品53件,B种纪念品47件时,获得最大利润是2530元。
种纪念品53件,B种纪念品47件时,获得最大利润是2530元。
-
科目: 来源: 题型:
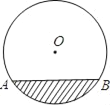
查看答案和解析>>【题目】某居民小区的一处圆柱形的输水管道破裂,维修人员为更换管道,需要确定管道圆形截面的半径.如图,若这个输水管道有水部分的水面宽AB=16cm,水最深的地方的高度为4cm,求这个圆形截面的半径.
-
科目: 来源: 题型:
查看答案和解析>>【题目】随着“互联网+”时代的到来,一种新型打车方式受到大众欢迎,该打车方式的总费用由里程费和耗时费组成,其中里程费按x元/公里计算,耗时费按y元/分钟计算(总费用不足9元按9元计价).小明、小刚两人用该打车方式出行,按上述计价规则,其打车总费用、行驶里程数与打车时间如表:
时间(分钟)
里程数(公里)
车费(元)
小明
8
8
12
小刚
12
10
16
(1)求x,y的值;
(2)如果小华也用该打车方式,打车行驶了11公里,用了14分钟,那么小华的打车总费用为多少?
-
科目: 来源: 题型:
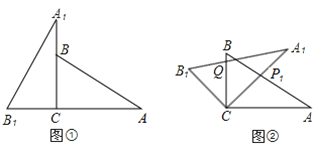
查看答案和解析>>【题目】将两块全等的三角板如图①摆放,其中∠A1CB1=∠ACB=90°,∠A1=∠A=30°.
(1)将图①中的△A1B1C顺时针旋转45°得图②,点P1是A1C与AB的交点,点Q是A1B1与BC的交点,求证:CP1=CQ;
(2)在图②中,若AP1=2,则CQ等于多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个不透明的袋子中装有红、白两种颜色的小球,这些球除颜色外完全相同,其中红球有
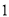 个,若从中随机摸出一个球,这个球是白球的概率为
个,若从中随机摸出一个球,这个球是白球的概率为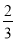 .
.(
 )请直接写出袋子中白球的个数.
)请直接写出袋子中白球的个数.(
 )随机摸出一个球后,放回并搅匀,再随机摸出一个球,求两次都摸到相同颜色的小球的概率.(请结合树状图或列表解答)
)随机摸出一个球后,放回并搅匀,再随机摸出一个球,求两次都摸到相同颜色的小球的概率.(请结合树状图或列表解答) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一个长方形运动场被分隔成
 、
、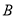 、
、 、
、 、
、 共
共 个区,
个区,  区是边长为
区是边长为 的正方形,
的正方形,  区是边长为
区是边长为 的正方形.
的正方形.(1)列式表示每个
 区长方形场地的周长,并将式子化简;
区长方形场地的周长,并将式子化简;(2)列式表示整个长方形运动场的周长,并将式子化简;
(3)如果
 ,
,  ,求整个长方形运动场的面积.
,求整个长方形运动场的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,AB∥DE,AC∥DF,AC=DF下列条件中,不能判断△ABC≌△DEF的是( )

A. AB=DE B. ∠B=∠E C. EF=BC D. EF∥BC
相关试题

