[题目]已知关于x的方程x2+2kx+k2+k+3=0的两根分别是x1.x2.则(x1﹣1)2+(x2﹣1)2的最小值是．题目和参考答案 ——青夏教育精英家教网—

【题目】已知关于x的方程x2+2kx+k2+k+3=0的两根分别是x1、x2，则（x1﹣1）2+（x2﹣1）2的最小值是_____．

【答案】8

【解析】∵关于x的方程x2+2kx+k2+k+3=0的两根分别是x1、x2，

∴x1+x2=﹣2k，x1x2=k2+k+3，

∵△=4k2﹣4（k2+k+3）=﹣4k﹣12≥0，解得k≤﹣3，

∴（x1﹣1）2+（x2﹣1）2

=x12﹣2x1+1+x22﹣2x2+1

=（x1+x2）2﹣2x1x2﹣2（x1+x2）+2

=（﹣2k）2﹣2（k2+k+3）﹣2（﹣2k）+2

=2k2+2k﹣4

=2（k+）2﹣

当k=-3时，（x1﹣1）2+（x2﹣1）2的值最小，最小为8.

故（x1﹣1）2+（x2﹣1）2的最小值是8．

故答案为：8．

相关试题

科目： 来源： 题型：

【题目】如图（1），一架长4米的梯子AB斜靠在与地面OM垂直的墙ON上，梯子与地面的倾斜角α为60°．
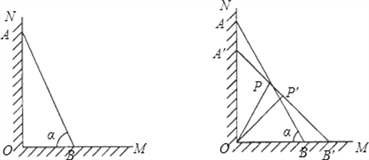
（1）求AO与BO的长；
（2）若梯子顶端A沿NO下滑，同时底端B沿OM向右滑行．如图（2），当A点下滑到A′点，B点向右滑行到B′点时，梯子AB的中点P也随之运动到P′点，若∠POP′=15°，试求AA′的长．
查看答案和解析>>
科目： 来源： 题型：

【题目】抛物线y=ax2+bx+c的顶点为D（﹣1，2），与x轴的一个交点A在点（﹣3，0）和（﹣2，0）之间，其部分图象如图，则以下结论：①b2﹣4ac＜0；②当x＞﹣1时，y随x增大而减小；③a+b+c＜0；④若方程ax2+bx+c﹣m=0没有实数根，则m＞2；　⑤3a+c＜0．其中正确结论的个数是（　　）
A. 2个 B. 3个 C. 4个 D. 5个
查看答案和解析>>
科目： 来源： 题型：

【题目】如图，△AOB的边OA半面镜．∠AOB＝36°，在OB边上有点E，从点E射出一束光线经平面镜反射后，反射光线DC恰好满足DC∥OB，已知入射光线、反射光线与半面镜的夹角相等，即∠ODE＝∠ADC，求∠DEB的度数．
查看答案和解析>>

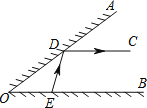
科目： 来源： 题型：

【题目】观察图形，解答问题：

（1）按下表已填写的形式填写表中的空格：

（2）请用你发现的规律求出图④中的数y和图⑤中的数x．

查看答案和解析>>

科目： 来源： 题型：

【题目】△ABC在平面直角坐标系中如图所示，
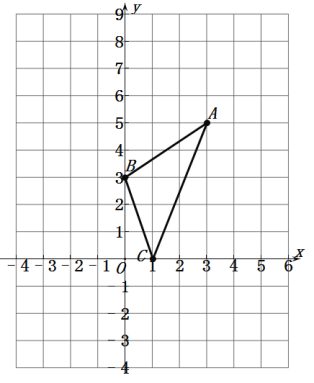
（1）S△ABC＝　．
（2）x轴上是否存在点P，使得S△BCP＝2S△ABC，若不存在，说明理由；若存在，求出P点的坐标．
（3）请直接写出：以A、B、C为顶点的平行四边形的第四个顶点D的坐标．
查看答案和解析>>
科目： 来源： 题型：

【题目】抚顺某中学为了解八年级学生的体能状况，从八年级学生中随机抽取部分学生进行体能测试，测试结果分为A，B，C，D四个等级．请根据两幅统计图中的信息回答下列问题：
（1）本次抽样调查共抽取了多少名学生？
（2）求测试结果为C等级的学生数，并补全条形图；
（3）若该中学八年级共有700名学生，请你估计该中学八年级学生中体能测试结果为D等级的学生有多少名？
（4）若从体能为A等级的2名男生2名女生中随机的抽取2名学生，做为该校培养运动员的重点对象，请用列表法或画树状图的方法求所抽取的两人恰好都是男生的概率．
查看答案和解析>>