【题目】如图,矩形ABCD的两边长AB=18cm,AD=4cm.点P、Q分别从A、B同时出发,P在边AB上沿AB方向以每秒2cm的速度匀速运动,Q在边BC上沿BC方向以每秒1cm的速度匀速运动,设运动时间为x秒,△PBQ的面积为y(cm2).

(1)求y关于x的函数关系式,并写出x的取值范围;
(2)求△PBQ的面积的最大值.
参考答案:
【答案】(1)y=-x2+9x(0<x≤4);(2)△PBQ的面积的最大值是20cm2.
【解析】试题分析:(1)分别表示出PB、BQ的长,然后根据三角形的面积公式列式整理即可得解;
(2)把函数关系式整理成顶点式解析式,然后根据二次函数的最值问题解答.
试题解析:(1)∵S△PBQ=![]() PB·BQ,
PB·BQ,
PB=AB-AP=18-2x,
BQ=x,
∴y=![]() (18-2x)x,
(18-2x)x,
即y=-x2+9x(0<x≤4);
(2)由(1)知:y=-x2+9x,
∴y=-(x-![]() )2+
)2+![]() ,
,
∵当0<x≤![]() 时,y随x的增大而增大,而0<x≤4,
时,y随x的增大而增大,而0<x≤4,
∴当x=4时,y最大值=20,
即△PBQ的最大面积是20cm2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在
 中,AB=AC,∠ABC =
中,AB=AC,∠ABC = ,D是BC边上一点,以AD为边作
,D是BC边上一点,以AD为边作 ,使AE=AD,
,使AE=AD, +
+ =180°.
=180°.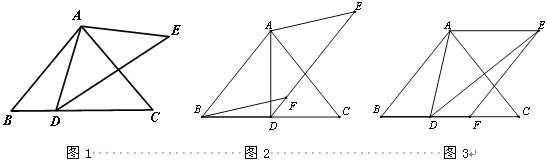
(1)直接写出∠ADE的度数(用含
 的式子表示);
的式子表示);(2)以AB,AE为边作平行四边形ABFE,
①如图2,若点F恰好落在DE上,求证:BD=CD;
②如图3,若点F恰好落在BC上,求证:BD=CF.
-
科目: 来源: 题型:
查看答案和解析>>【题目】明代数学家程大位所著的《算法统宗》全称《直指算法统宗》,是中国古代数学名著.某数学兴趣小组发现《算法统宗》里有这样一首诗:我问开店李三公,众客都来到店中,一房七客多七客,一房九客一房空.诗中后两句的意思是:如果每一间客房住7人,那么有7人无房可住;如果每一间客房住9人,那么就空出一间房.
(1)请列方程组,并求出该店有客房多少间?房客多少人?
(2)假设店主李三公将客房进行改造后,共有50间客房.每间客房收费30钱,且每间客房最多人住3人,一次性定客房25间以上(含25间),房费按8折优惠.若诗中“众客”再次一起入住,他们如何订房更合算?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形
 中,点
中,点 、
、 分别在边
分别在边 、
、 上,且
上,且 .下列结论:①
.下列结论:① ;②
;② ;③
;③ ;④
;④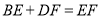 ;其中正确的是________(只填写序号).
;其中正确的是________(只填写序号).
-
科目: 来源: 题型:
查看答案和解析>>【题目】2019年我省开展了以“改革创新、奋发有为”为主题的大讨论活动,活动中某社区为了调查居民对社区服务的满意度,随机抽取了社区部分居民进行问卷调查;用
 表示“很满意”,
表示“很满意”, 表示“满意”,
表示“满意”, 表示“比较满意”,
表示“比较满意”, 表示“不满意”,如图是工作人员根据问卷调查统计资料绘制的两幅不完整的统计图.
表示“不满意”,如图是工作人员根据问卷调查统计资料绘制的两幅不完整的统计图.
请你根据统计图提供的信息解答以下问题:
(1)本次问卷调查共调查了多少个居民?
(2)求出调查结果为
 的人数,并将直方图中
的人数,并将直方图中 部分的图形补充完整;
部分的图形补充完整;(3)如果该社区有居民8000人,请你估计对社区服务感到“不满意”的居民约有多少人?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形
 的边长是4,
的边长是4, 的平分线交
的平分线交 于点
于点 ,若点
,若点 、
、 分别是
分别是 和
和 上的动点,则
上的动点,则 的最小值是__________.
的最小值是__________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某中学1000名学生参加了“环保知识竞赛”,为了了解本次竞赛成绩情况,从中抽取了部分学生的成绩(得分取整数,满分为100分)作为样本进行统计,并制作了如图频数分布表和频数分布直方图(不完整且局部污损,其中“■”表示被污损的数据).请解答下列问题:
成绩分组
频数
频率
50≤x<60
8
0.16
60≤x<70
12
a
70≤x<80
■
0.5
80≤x<90
3
0.06
90≤x<90
b
c
合计
■
1
(1)写出
 ,
, ,
, 的值;
的值;(2)请估计这1000名学生中有多少人的竞赛成绩不低于70分;
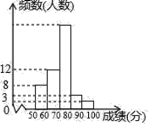
相关试题

