【题目】如图1,在![]() 中,AB=AC,∠ABC =
中,AB=AC,∠ABC =![]() ,D是BC边上一点,以AD为边作
,D是BC边上一点,以AD为边作![]() ,使AE=AD,
,使AE=AD,![]() +
+![]() =180°.
=180°.
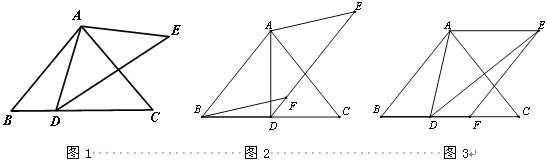
(1)直接写出∠ADE的度数(用含![]() 的式子表示);
的式子表示);
(2)以AB,AE为边作平行四边形ABFE,
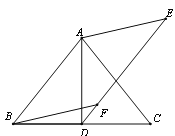
①如图2,若点F恰好落在DE上,求证:BD=CD;
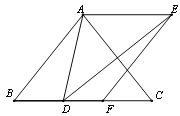
②如图3,若点F恰好落在BC上,求证:BD=CF.
参考答案:
【答案】(1)![]() ;(2)证明见解析.
;(2)证明见解析.
【解析】
试题(1)由在△ABC中,AB=AC,∠ABC=α,可求得∠BAC=180°-2α,又由AE=AD,∠DAE+∠BAC=180°,可求得∠DAE=2α,继而求得∠ADE的度数;
(2)①由四边形ABFE是平行四边形,易得∠EDC=∠ABC=α,则可得∠ADC=∠ADE+∠EDC=90°,证得AD⊥BC,又由AB=AC,根据三线合一的性质,即可证得结论;
②由在△ABC中,AB=AC,∠ABC=α,可得∠B=∠C=α,四边形ABFE是平行四边形,可得AE∥BF,AE=BF.即可证得:∠EAC=∠C=α,又由(1)可证得AD=CD,又由AD=AE=BF,证得结论.
试题解析:(1)∠ADE =![]() .
.
(2)①证明:∵四边形ABFE是平行四边形,
∴AB∥EF.
∴![]() .
.
由(1)知,∠ADE =![]() ,
,
∴![]() .
.
∴AD⊥BC.
∵AB=AC,
∴BD=CD.
②证明:
∵AB=AC,∠ABC =![]() ,
,
∴![]() .
.
∵四边形ABFE是平行四边形,
∴AE∥BF,AE=BF.
∴![]() .
.
由(1)知,![]() ,
,
∴![]() .
.
∴![]() .
.
∴AD=CD.
∵AD=AE=BF,
∴BF=CD.
∴BD=CF.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知等腰三角形ABC的底角为30°,以BC为直径的⊙O与底边AB交于点D,过D作DE⊥AC,垂足为E.
(1)证明:DE为⊙O的切线;
(2)连接OE,若BC=4,求△OEC的面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】(本小题满分8分)某厂制作甲、乙两种环保包装盒。已知同样用6m的材料制成甲盒的个数比制成乙盒的个数少2个,且制成一个甲盒比制作一个乙盒需要多用20%的材料。
(1)求制作每个甲盒、乙盒各用多少材料?
(2)如果制作甲、乙两种包装盒3000个,且甲盒的数量不少于乙盒数量的2倍,那么请写出所需材料总长度
 与甲盒数量
与甲盒数量 之间的函数关系式,并求出最少需要多少米材料。
之间的函数关系式,并求出最少需要多少米材料。 -
科目: 来源: 题型:
查看答案和解析>>【题目】为了解某校学生的身高情况,王老师随机抽取该校男生、女生进行抽样调查,已知抽取的样本中,男生、女生人数相同,利用所得数据绘制如下统计图表:
组别
身高
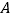
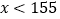
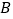
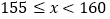
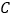
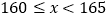
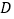
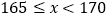

身高情况分组表
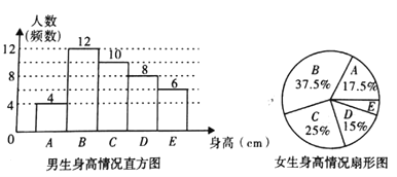
根据图表提供的信息,回答下列问题:
(1)样本中,女生身高在
 组的人数有_________人;
组的人数有_________人;(2)在上面的扇形统计图中,表示
 组的扇形的圆心角是_________°;
组的扇形的圆心角是_________°;(3)已知该校共有男生800人,女生760人,请估计该校身高在
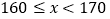 之间的学生约有多少人?
之间的学生约有多少人? -
科目: 来源: 题型:
查看答案和解析>>【题目】明代数学家程大位所著的《算法统宗》全称《直指算法统宗》,是中国古代数学名著.某数学兴趣小组发现《算法统宗》里有这样一首诗:我问开店李三公,众客都来到店中,一房七客多七客,一房九客一房空.诗中后两句的意思是:如果每一间客房住7人,那么有7人无房可住;如果每一间客房住9人,那么就空出一间房.
(1)请列方程组,并求出该店有客房多少间?房客多少人?
(2)假设店主李三公将客房进行改造后,共有50间客房.每间客房收费30钱,且每间客房最多人住3人,一次性定客房25间以上(含25间),房费按8折优惠.若诗中“众客”再次一起入住,他们如何订房更合算?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形
 中,点
中,点 、
、 分别在边
分别在边 、
、 上,且
上,且 .下列结论:①
.下列结论:① ;②
;② ;③
;③ ;④
;④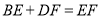 ;其中正确的是________(只填写序号).
;其中正确的是________(只填写序号).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形ABCD的两边长AB=18cm,AD=4cm.点P、Q分别从A、B同时出发,P在边AB上沿AB方向以每秒2cm的速度匀速运动,Q在边BC上沿BC方向以每秒1cm的速度匀速运动,设运动时间为x秒,△PBQ的面积为y(cm2).

(1)求y关于x的函数关系式,并写出x的取值范围;
(2)求△PBQ的面积的最大值.
相关试题

