【题目】计算下列各题
(1)化简:( ![]() ﹣1)÷
﹣1)÷ ![]()
(2)关于x的一元二次方程kx2+2x﹣3=0有两个不相等的实数根,求k的取值范围.
参考答案:
【答案】
(1)解:原式=( ![]() ﹣
﹣ ![]() )
) ![]()
=﹣ ![]()
![]()
=﹣ ![]()
(2)解:∵关于x的一元二次方程kx2+2x﹣3=0有两个不相等的实数根,
∴k≠0,且△>0,即22﹣4×k×(﹣3)>0,
解得k>﹣ ![]() 且k≠0
且k≠0
【解析】(1)先将括号内的式子通分,再将除法转化为乘法,然后约分计算即可;(2)根据一元二次方程的定义以及根的判别式得到k≠0且△>0,即22﹣4×k×(﹣3)>0,然后解两个不等式即可得到k的取值范围.
【考点精析】解答此题的关键在于理解分式的混合运算的相关知识,掌握运算的顺序:第一级运算是加法和减法;第二级运算是乘法和除法;第三级运算是乘方.如果一个式子里含有几级运算,那么先做第三级运算,再作第二级运算,最后再做第一级运算;如果有括号先做括号里面的运算.如顺口溜:"先三后二再做一,有了括号先做里."当有多层括号时,先算括号内的运算,从里向外{[(?)]},以及对求根公式的理解,了解根的判别式△=b2-4ac,这里可以分为3种情况:1、当△>0时,一元二次方程有2个不相等的实数根2、当△=0时,一元二次方程有2个相同的实数根3、当△<0时,一元二次方程没有实数根.
-
科目: 来源: 题型:
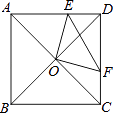
查看答案和解析>>【题目】如图,在正方形ABCD中,O是对角线的交点,过点O作OE⊥OF,分别交AD,CD于E,F,若AE=6,CF=4,则EF= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图放置的△OAB1 , △B1A1B2 , △B2A2B3 , …都是边长为2的等边三角形,点A在x轴上,点O,B1 , B2 , B3 , …都在正比例函数y=kx的图象l上,则点B2017的坐标是 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,等腰三角形ABC中,AB=AC,D、E都在BC上,要使△ABD≌△ACE,需要添加一个条件,某学习小组在讨论这个条件时给出了如下几种方案: ①AD=AE;②BD=CE;③BE=CD;④∠BAD=∠CAE,其中可行的有( )
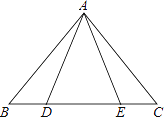
A. 1种 B. 2种 C. 3种 D. 4种
-
科目: 来源: 题型:
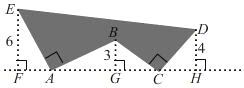
查看答案和解析>>【题目】如图,EF、BG、DH 都垂直于 FH,AE⊥AB 且 AE=AB,BC⊥CD 且 BC=CD,请按照图中所标注的数据,计算图中阴影部分的面积 S 是_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】随着全国各地空气出现严重污染,PM2.5屡屡爆表,我国多个城市发生雾霾天气,越来越多的人开始关注一个原本陌生的术语﹣PM2.5.某校九年级共有1000名学生,团委准备调查他们对“PM2.5”知识的了解程度.
(1)在确定调查方式时,团委设计了以下三种方案: 方案一:调查九年级部分女生;
方案二:调查九年级部分男生;
方案三:到九年级每个班去随机调查一定数量的学生.
请问其中最具有代表性的一个方案是;
(2)团委采用了最具有代表性的调查方案,并用收集到的数据绘制出两幅不完整的统计图,请你根据图中信息,将其补充完整;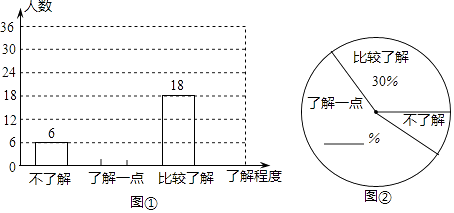
(3)请你估计该校九年级约有多少名学生比较了解“PM2.5”的知识. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四边形ABCD中,AD∥BC,E为CD的中点,连接AE、BE,BE⊥AE,延长AE交BC的延长线于点F.
求证:(1)FC=AD;
(2)AB=BC+AD.

相关试题

