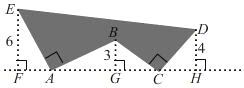
【题目】如图,EF、BG、DH 都垂直于 FH,AE⊥AB 且 AE=AB,BC⊥CD 且 BC=CD,请按照图中所标注的数据,计算图中阴影部分的面积 S 是_____.
参考答案:
【答案】50
【解析】
由 AE⊥AB,EF⊥FH,BG⊥AG,可以得到∠EAF=∠ABG,而 AE=AB,∠
EFA=∠AGB,由此可以证明△EFA≌△ABG,所以 AF=BG,AG=EF; 同理证得△BGC≌△DHC,GC=DH,CH=BG.故 FH=FA+AG+GC+CH=3+6+4+3=16,然后利用面积的割补法和面积公式即可求出图形的面积.
∵AE⊥AB 且 AE=AB,EF⊥FH,BG⊥FH
∴∠EAB=∠EFA=∠BGA=90°,
∵∠EAF+∠BAG=90°,∠ABG+∠BAG=90°
∴∠EAF=∠ABG,
∴AE=AB,∠EFA=∠AGB,∠EAF=∠ABG
∴△EFA≌△ABG(AAS)
∴AF=BG,AG=EF.
同理证得△BGC≌△DHC(AAS)得 GC=DH,CH=BG. 故 FH=FA+AG+GC+CH=3+6+4+3=16,
故 S=![]() (6+4)×16﹣3×4﹣6×3=50.
(6+4)×16﹣3×4﹣6×3=50.
故答案为:50.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图放置的△OAB1 , △B1A1B2 , △B2A2B3 , …都是边长为2的等边三角形,点A在x轴上,点O,B1 , B2 , B3 , …都在正比例函数y=kx的图象l上,则点B2017的坐标是 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,等腰三角形ABC中,AB=AC,D、E都在BC上,要使△ABD≌△ACE,需要添加一个条件,某学习小组在讨论这个条件时给出了如下几种方案: ①AD=AE;②BD=CE;③BE=CD;④∠BAD=∠CAE,其中可行的有( )
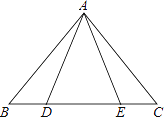
A. 1种 B. 2种 C. 3种 D. 4种
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算下列各题
(1)化简:(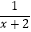 ﹣1)÷
﹣1)÷ 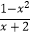
(2)关于x的一元二次方程kx2+2x﹣3=0有两个不相等的实数根,求k的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】随着全国各地空气出现严重污染,PM2.5屡屡爆表,我国多个城市发生雾霾天气,越来越多的人开始关注一个原本陌生的术语﹣PM2.5.某校九年级共有1000名学生,团委准备调查他们对“PM2.5”知识的了解程度.
(1)在确定调查方式时,团委设计了以下三种方案: 方案一:调查九年级部分女生;
方案二:调查九年级部分男生;
方案三:到九年级每个班去随机调查一定数量的学生.
请问其中最具有代表性的一个方案是;
(2)团委采用了最具有代表性的调查方案,并用收集到的数据绘制出两幅不完整的统计图,请你根据图中信息,将其补充完整;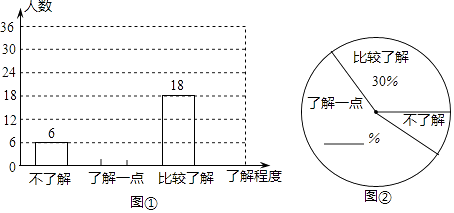
(3)请你估计该校九年级约有多少名学生比较了解“PM2.5”的知识. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四边形ABCD中,AD∥BC,E为CD的中点,连接AE、BE,BE⊥AE,延长AE交BC的延长线于点F.
求证:(1)FC=AD;
(2)AB=BC+AD.

-
科目: 来源: 题型:
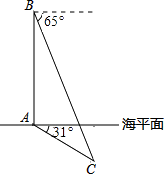
查看答案和解析>>【题目】在某次反潜演习中,红方军舰A测得蓝方潜艇C的俯角为31°,位于军舰A正上方800米的红方反潜直升机B测得潜艇C的俯角为65°.试根据以上数据求出潜艇C离开海平面的下潜深度(结果保留整数)
(参考数据:sin31°≈ ,tan31°≈
,tan31°≈ 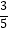 ,sin65°≈
,sin65°≈  ,tan65°≈
,tan65°≈ 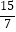 )
)
相关试题

